Moon Earth and Satellite gravitation

[Frozen Light]

Homework Statement

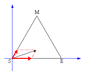
At a certain instant, the earth, the moon, and a stationary 1030kg spacecraft lie at the vertices of an equilateral triangle whose sides are 3.84×10^5km in length.

Find the magnitude of the net gravitational force exerted on the spacecraft by the Earth and moon.

Homework Equations

GMm/r^2 = Fg

r = 3.84*10^5 km
Me = 5.98*10^24 kg
Mm = 7.35*10^22 kg
G = 6.67*10^-11
Ms = 1030kg

The Attempt at a Solution

http://imgur.com/p8OBdfd
I think it's probably a simple error somewhere but I've gotten about 3-4 different answers all which are not F=2.8N - I've tried calculating it at different stages in the algebra - are the angles somehow not based off 60*? I don't know what it's missing.

 

[gneill]

Homework Statement

At a certain instant, the earth, the moon, and a stationary 1030kg spacecraft lie at the vertices of an equilateral triangle whose sides are 3.84×105km in length.

Is there a question to go along with this statement?

 

[Frozen Light]

OH, sorry.

Find the magnitude of the net gravitational force exerted on the spacecraft by the Earth and moon. - edited it it in the first post too

edit: also that it's not 3.84×105km - it's 3.84 x 10^5km

edit: in the image I accidentally dropped the squares around [[ROOT][Cos60(Me - Mm)^2 + Sin60(Me+Mm)^2] but added them in my calculation

 

[gneill]

You're probably making your life more difficult than you have to by placing the satellite at the top of the triangle and making your coordinate system pass through it. Instead, try placing the satellite at the origin and the other two bodies at the other vertexes like this:

This way only one of the forces (F_SM) will have two components.

I'd expect the net force magnitude to be just a few Newtons.

 

[Frozen Light]

The answer is 2.8N - I'm trying to match my answer to that one.
But I don't really understand what you mean.

Do you mean just line one of the sides with an axis?

(Triangle)
Me
M mS

So that there is no Xdir force from Me?

 

[gneill]

The idea is to choose the axes so that one of the forces lies entirely along an axis so it has only one component (the other being zero). Then you only need concern yourself with the individual components of the other force.

Looking at your solution, it appears that you aren't squaring the sin and cos values when you take the sum of squares of the components.

 

[Frozen Light]

Yes, that was it. Thank you.

I'm not sure how I didn't see that after spending that much time looking at it haha.

 

[gneill]

Yes, that was it. Thank you.

I'm not sure how I didn't see that after spending that much time looking at it haha.

The most insidious errors are the ones that hidden in plain sight It often just takes a fresh pair of eyes to spot them.