More (VERY BASIC) Questions on Example on Wedge Products

[Math Amateur]

I am reading Barrett O'Neil's book: Elementary Differential Geometry ...

I need help with some more issues/problems with the example on wedge products of differential forms in O'Neill's text on page 31 in Section 1.6 ..The example reads as follows:

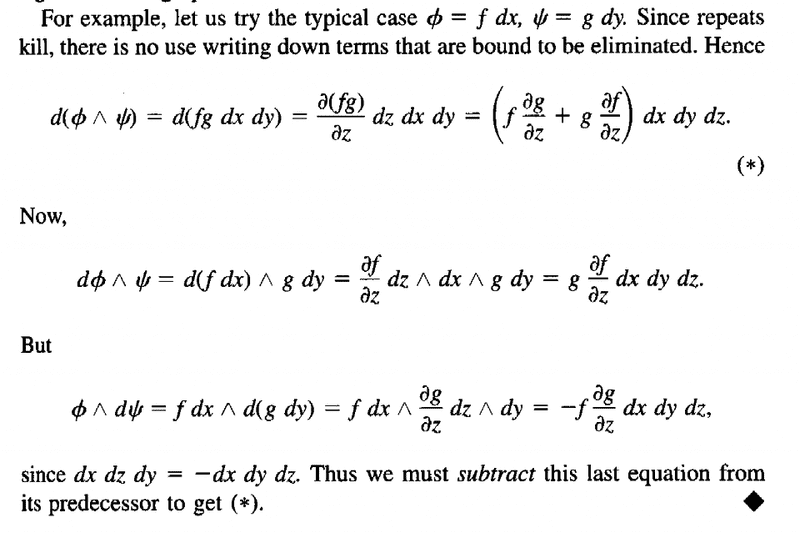In my working of the example above ... trying to understand (*) ... I proceeded as follows ... but had some questions almost immediately ...

We have $\phi = f \ dx$ and $\psi = g \ dy$so we can write (can we?)$d ( \phi \wedge \psi ) = d( f \ dx \wedge \ g \ dy )$$= d (f \ dx \ g \ dy )$But is this last step correct? That is is the wedge product of these elements just a concatenation? If so, why?
Continuing ...

$d (f \ dx \ g \ dy ) = d( fg \ dx \ dy )$

Is this correct? Why?
It assumes all these type of elements commute ... is that correct? Why?... I am also perplexed by what is happening (and the justification) in O'Neill's step in (*) where he writes:

$d(fg \ dx \ dy ) = \partial (fg) / \partial z \ dz \ dx \ dy$Can someone explain and justify this step please ... preferably by providing all the intervening steps and their justification ...
Hope someone can help with these questions/issues/problems ...

Peter

 

[andrewkirk]

d(f dx g dy)=d(fg dx dy)

Is this correct? Why?
It assumes all these type of elements commute ... is that correct? Why?

I can do the middle one, as it's very quick, and I only have a minute right now.
f and g are scalars, whereas dx and dy are one-forms, which are elements of a vector space. As is usual with vector spaces, we can move scalars around as much as we like, and that's what's done above. However the vectors / one-forms dx and dy do not commute with each other (in fact if you change the order you change the sign - they anti-commute), so their order cannot be changed.
Hope that helps.

 

[Math Amateur]

I can do the middle one, as it's very quick, and I only have a minute right now.
f and g are scalars, whereas dx and dy are one-forms, which are elements of a vector space. As is usual with vector spaces, we can move scalars around as much as we like, and that's what's done above. However the vectors / one-forms dx and dy do not commute with each other (in fact if you change the order you change the sign - they anti-commute), so their order cannot be changed.
Hope that helps.

Thanks Andrew ... yes, most helpful

Peter