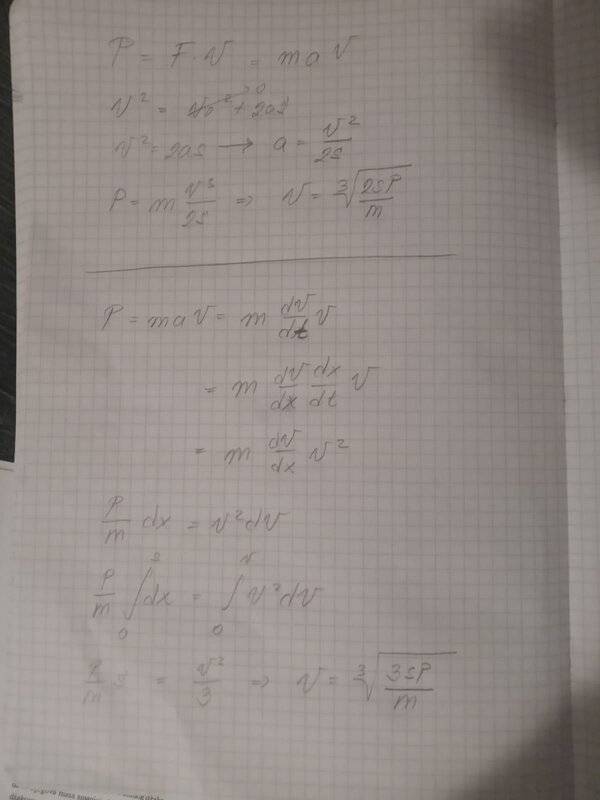Weber_per_metermeter
- 2
- 1
- Homework Statement
- In horizontal straight line path, there's a car, weighing 600kg, fully powered with P=25kW, that is constant during motion. Car is starting from rest state (v0=0). What is the speed intensity after s=125m of driving? Enviromental resistance and friction are negligible.
- Relevant Equations
- P=F*v=m*a*v
v^2=v0^2+2as
So I tried to solve this in two methods, but I keep getting different results, and I don't know why.