SUMMARY
The discussion focuses on deriving the motion equations for a double pendulum using Newton's formalism, contrasting it with Lagrange's approach. The user, @Daniel Boy, has already established a Lagrangian but struggles to obtain the second equation using Newton's method. The forum participants suggest employing a torque equation for the entire system and a separate one for the lower rod, emphasizing the need to account for fictitious forces due to acceleration in the coordinate system. The complexity of the algebra involved in this derivation is acknowledged.
PREREQUISITES
- Understanding of Newton's laws of motion
- Familiarity with Lagrangian mechanics
- Knowledge of free body diagrams
- Basic concepts of torque and fictitious forces
NEXT STEPS
- Study the derivation of motion equations using Newton's formalism for a double pendulum
- Explore the application of fictitious forces in accelerating reference frames
- Review examples of torque equations in multi-body systems
- Investigate the differences between Lagrangian and Newtonian mechanics in complex systems
USEFUL FOR
Students and professionals in physics, particularly those studying classical mechanics, as well as engineers and researchers working on dynamic systems involving pendulums.
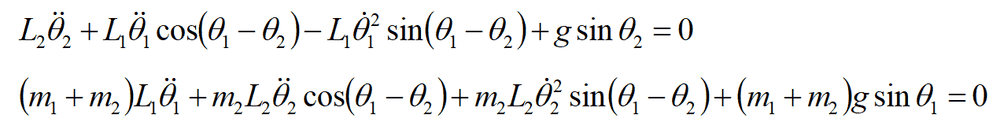
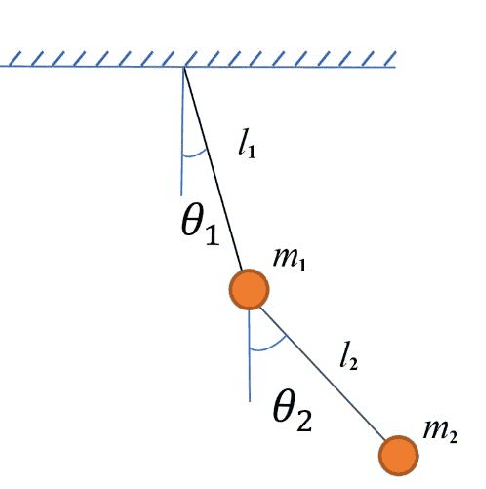
 ##\qquad## !
##\qquad## !