- #1
FEAnalyst
- 342
- 144
- TL;DR Summary
- Which formula will give correct results for the maximum velocity of a pendulum taking into account both rod and bob?
Hi,
I'm working on a simple benchmark problem for FEA. It's a pendulum initially positioned at an angle of ##45^{\circ}## and then subjected to gravity. I'm interested in the maximum velocity (when the pendulum is in the vertical position). So far, I've been using this formula: $$v=\omega \cdot l=\sqrt{\frac{3g}{l} \cdot \left( \cos{\left( \theta_{start} \right)}- cos{\left(\theta_{end} \right)} \right)} \cdot l$$ where: ##l## - pendulum length, ##g## - gravitational acceleration, ##\theta_{start}=45^{\circ}## - starting angle, ##\theta_{end}=180^{\circ}## - final angle. The geometry was just a cuboid (here shown from the side):
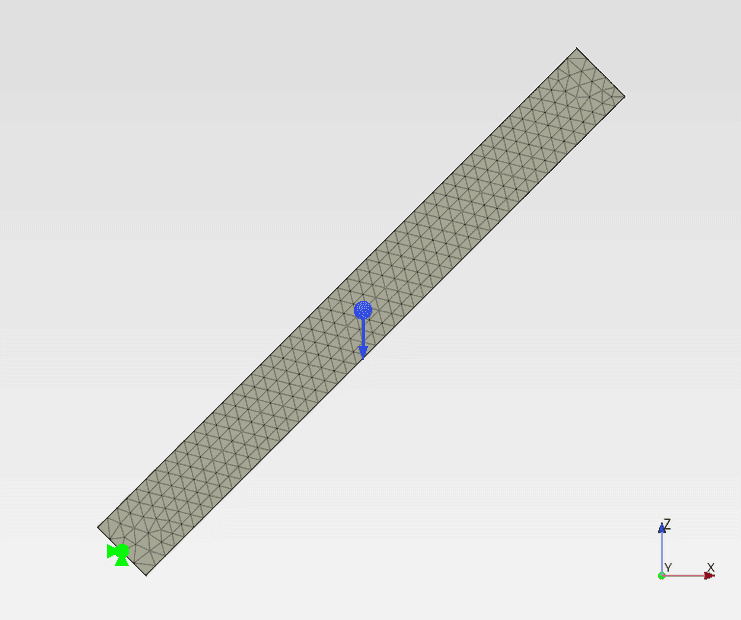
I obtained a very good agreement between FEA and hand calculation for this case. But now I'd like to change the geometry to more pendulum-like:

The problem is that the aforementioned formula doesn't provide correct results for this case, even though it only needs the pendulum length, not mass as input. I've been looking for some equations for compound physical pendulums since the geometry above likely represents this kind of problem, but I haven't found any formulas equivalent to the one I've been using so far (for the maximum velocity based on angles). In FEA, I can't make the rod massless so I may have to account for the masses of both components even when the rod is very thin.
Do you know where I can find such a formula ? Should I change the assumptions for the analytical calculations ?
I'm working on a simple benchmark problem for FEA. It's a pendulum initially positioned at an angle of ##45^{\circ}## and then subjected to gravity. I'm interested in the maximum velocity (when the pendulum is in the vertical position). So far, I've been using this formula: $$v=\omega \cdot l=\sqrt{\frac{3g}{l} \cdot \left( \cos{\left( \theta_{start} \right)}- cos{\left(\theta_{end} \right)} \right)} \cdot l$$ where: ##l## - pendulum length, ##g## - gravitational acceleration, ##\theta_{start}=45^{\circ}## - starting angle, ##\theta_{end}=180^{\circ}## - final angle. The geometry was just a cuboid (here shown from the side):
I obtained a very good agreement between FEA and hand calculation for this case. But now I'd like to change the geometry to more pendulum-like:
The problem is that the aforementioned formula doesn't provide correct results for this case, even though it only needs the pendulum length, not mass as input. I've been looking for some equations for compound physical pendulums since the geometry above likely represents this kind of problem, but I haven't found any formulas equivalent to the one I've been using so far (for the maximum velocity based on angles). In FEA, I can't make the rod massless so I may have to account for the masses of both components even when the rod is very thin.
Do you know where I can find such a formula ? Should I change the assumptions for the analytical calculations ?