Motion when 2D forces are exerted on masses at each end of a baton?

[mikejm]

Let's say you have a simple structure with two equal masses connected by a massless rigid baton of length L. Like this:

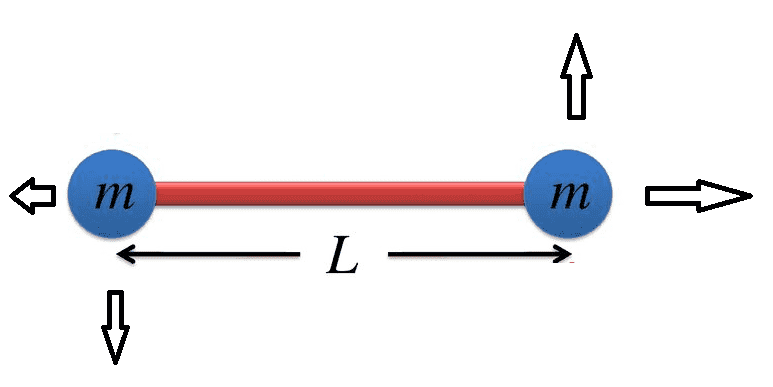
Imagine this structure is totally free in space. It is not hinged in any way. Then forces act on each mass in 2D (x,y). If you have the x and y force vectors acting on each mass, and knowing the two masses are linked, can you calculate the net acceleration of each mass that results?

ie. If you have:

L = length connecting masses
Fm1X = x-axis force on mass 1
Fm1Y = y-axis force on mass 1
Fm2X = x-axis force on mass 2
Fm2Y = y-axis force on mass 2

And the initial (x,y) coordinates of the two masses and their initial velocities, can you calculate the accelerations and new velocities after a certain increment of time?

Numerical solution is fine. Would want to be able to solve such a problem at an audio sample rate recursively for 100 similar elements per sample or so. At each sample I'd recalculate the x and y forces acting on each mass, then need to determine their new velocities/accelerations for the next time increment.

Obviously this would be trivial for a mass that is not connected to another in this way. I'm not sure how to take into account that they must remain a fixed distance apart (ie. linked by the "baton").

Thanks.

 

[PeroK]

Obviously this would be trivial for a mass that is not connected to another in this way. I'm not sure how to take into account that they must remain a fixed distance apart (ie. linked by the "baton").

Thanks.

That means the two masses are an extended rigid body. You still have Newton's second law for the net (or total force) and the acceleration of the centre of mass (CoM):
$$\vec F_{total} = M_{total} \ \vec a_{CoM}$$
And you also have the rotational motion given by the total torque about the centre of mass $\tau$, moment of inertia $I$ of the body, and angular acceleration about the centre of mass, $\alpha$.
$$\vec \tau = I \ \vec \alpha$$
These two equations together describe the motion of the object in terms of: motion of centre of mass and rotation about the centre of mass.

 

[Lnewqban]

...
I'm not sure how to take into account that they must remain a fixed distance apart (ie. linked by the "baton").

You have a solid body with forces applied to two different locations, which happen to be where most of the mass is also located at.
The massless connection is still a solid part of the body, since it transfers lineal forces and moments between both masses.
That body will behave based on resultant forces and their on their distances and directions respect to the center of mass of the system.