Solving the N Body Problem with RK4: Verification & Convergence

[DivergentSpectrum]

the force field trajectory calculator worked pretty good, so i decided to step it up and solve the famous n body problem.

i used rk4 to solve it, and to verify my solution i calculate the work done on each particle and the kinetic energy of each particle at the beginning and end.
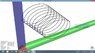
it appears to converge pretty nicely when one object is very massive compared to the other, but i notice some strange behavior otherwise. for one, i always thought a 2 body system would be two elipses sharing a focus (barycenter), but instead i get all kinds of different shapes.
also the energy diverges in more "dynamic" systems.
How does one calculate the "total conserved energy" of a system? (or analogous conserved quantities such as angular momentum) i had been just using the work energy theorem, (line integral of force equals change in kinetic energy) but I am not sure if that still holds when the force depends on the location of an object, that is also experiencing a force due to the same object.
do these pictures qualitatively look like a 2 body system?

edit: in each of these the blue particles initial velocity is 0, and the black particles initial velocity is non zero. the step size is the same, but the mass of the black particle is different. the more "chaotic" looking patterns have a larger mass set for the black particle(up to where the masses are equal)

 

[willem2]

edit: in each of these the blue particles initial velocity is 0, and the black particles initial velocity is non zero. the step size is the same, but the mass of the black particle is different. the more "chaotic" looking patterns have a larger mass set for the black particle(up to where the masses are equal)

If the total initial momentum isn't zero, the center of mass will keep moving, and you get spirals instead of ellipses. You'll need to set v_1 = - \frac {m_2 }{m_1} v_2 with 2 bodies to get a momentum of 0.

 

[DivergentSpectrum]

thanks, i had a feeling the system as a whole might be undergoing some kind of translational motion. as far as the divergences go i might just be expecting too much from a numerical method.