Need a little help with motion on an inclined plane

[inv4lid]

Homework Statement

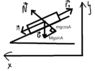
On a plane tilted at the angle of 30 degrees with the horizon lies an object, whose weight is equal to 1.4 kg. The coefficient of friction between the object and the plane is equal to 0.2. Find acceleration.

m = 1,4kg; (weight)
Angle (A) = 30 degrees.
COF µ = 0,2
Ff - friction force
N - reaction
F1 - force that moves the object (the very-right one)
__________________________________________
find acceleration.

Homework Equations

(vector form of resultant force) Ff + N + G + F1 = m*a;

The Attempt at a Solution

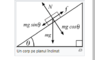
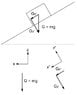
I have tried to project forces' vectors on OX and OY axis.
Projecting on OX we get:
Nx = N;
Gx = 0;
F1x = -F1; (against OX)
Ffx = G*sinA;
Using that data, we can obtain something like that:
N + G*sinA - F1 = m*a;Projecting on OY we get:
a = 0;
F1 = 0;
Ny = mgcosA;
Gy = -mg;
Ffy = 0;
-> mgcosA - mg = 0 ; - somehow weird, correct me pls.
I'm also not sure about the N projected on OX.
ty in advance!

 

[stockzahn]

You want to find the acceleration parallel to the surface the object is gliding on (30° angle to the horizontal), correct? Then it is easier to project the forces on a rotated coordinate system parallel to the surface and normal to it (according to the directions of your forces $N$ and $F$).

What are the forces $F_f$ and $F_1$? Your $N$ does not act orthogonally on the surface. Did you draw it like that on purpose?

 

[inv4lid]

Did you draw it like that on purpose?

I just tried to draw same thing that's on wiki. My img can possibly be imprecise, as i don't really get what is the line mg*cosA represents...

You want to find the acceleration parallel to the surface the object is gliding on (30° angle to the horizontal), correct?

Yes.

 

[stockzahn]

View attachment 218590
I just tried to draw same thing that's on wiki. My img can possibly be imprecise, as i don't really get what is the line mg*cosA represents...

In a coordinate system with a horizontal and a vertical axis ($x$,$z$ in my drawing below), the weight force $G=mg$ is parallel to the $z$-axis and points downwards. Now you want to calculate the motion parallel to the surface (since the box cannot/does not move normal to it). Therefore you change the coordinate system rotated by the angle $\Theta$ ($x'$,$z'$ in my drawing below), where the surface is parallel to the $x'$-axis. Now you want to transform the force $G$ into the new coordinate system by finding two orthogonal forces (vectors), whose sum yields the original force $G$. This can be done using trigonometry. The component of $G$ pointing parallel to the surface can be calculated with $G_{x'}=mg sin\Theta$, the component of $G$ pointing orthogonally to the surface can be calculated with $G_{z'}=mg cos\Theta$. The sum of the two forces (vectors) results in the original force $G$.

Is this explanation sufficient to understand the components $mg sin\Theta$ and $mg cos\Theta$?

 

[haruspex]

Nx = N;

That would say the normal force is horizontal. Clearly it is not. What component of the normal force acts in the X direction?

F1 - force that moves the object (the very-right one)

Do you mean that F1 is the net force? You have that pointing up the slope, and the friction force pointing down(!)

Ffx = G*sinA;

You do not seem to understand friction. You should have listed a relevant equation for this: the kinetic friction force is the coefficient of kinetic friction multiplied by the normal force, F_k=μ_kN.

 

[haruspex]

View attachment 218590
I just tried to draw same thing that's on wiki. My img can possibly be imprecise, as i don't really get what is the line mg*cosA represents.

The diagram is a little confusing because it fails to distinguish between applied forces and their resolution into components. There are only the three applied forces, mg, N and f. You can replace mg by mg sin(θ) and mg cos(θ), but it is a bit misleading to show these as well as the original mg all on the same diagram, all using the same style of line and arrow.