- #1
Jite
- 2
- 0
Good afternoon, I am having some trouble solving this basic fluids problem, and I am hoping you can look over my work, and offer some assistance.
A submarine has a total mass of 2.1 multiplied by 10^6 kg, including crew and equipment. The vessel consists of two parts, the pressure hull, which has a volume of 2 multiplied by 10^3 m^3, and the ballast tanks, which have a volume of 6 multiplied by 10^2 m^3. When the sub cruises on the surface, the ballast tanks are filled with air. When cruising below the surface, seawater is admitted into the tanks. (Neglect the mass of air in the tanks and use 1.025 as the specific gravity of seawater.)
What fraction of the submarine's volume is above the water surface when the tanks are filled with air? (%)
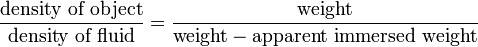
First I set the right hand side of the equation to 1, since the apparent weight will be zero because the submarine is floating on the surface and their will be no experienced force.
Therefore I have
p(sub) = p(sea water)
m(sub) / Volume (sub) = density of water
m(sub) / density of water = Volume of Sub Submerged in Water.
or
Volume Sub Submerged in water (m^3) = 2.1*10^9 g / (1.025*(1000*1000*1000) g/m^3)
But I get a Volume of 2.04 m^3,
or ~1% of the sub is submerged and ~99% of the sub is above water.
This answer is incorrect, and is intuitively wrong as I don't think a 200,000 kg 2m^3 block would float.
Thanks in advance for your help
Homework Statement
A submarine has a total mass of 2.1 multiplied by 10^6 kg, including crew and equipment. The vessel consists of two parts, the pressure hull, which has a volume of 2 multiplied by 10^3 m^3, and the ballast tanks, which have a volume of 6 multiplied by 10^2 m^3. When the sub cruises on the surface, the ballast tanks are filled with air. When cruising below the surface, seawater is admitted into the tanks. (Neglect the mass of air in the tanks and use 1.025 as the specific gravity of seawater.)
What fraction of the submarine's volume is above the water surface when the tanks are filled with air? (%)
Homework Equations
The Attempt at a Solution
First I set the right hand side of the equation to 1, since the apparent weight will be zero because the submarine is floating on the surface and their will be no experienced force.
Therefore I have
p(sub) = p(sea water)
m(sub) / Volume (sub) = density of water
m(sub) / density of water = Volume of Sub Submerged in Water.
or
Volume Sub Submerged in water (m^3) = 2.1*10^9 g / (1.025*(1000*1000*1000) g/m^3)
But I get a Volume of 2.04 m^3,
or ~1% of the sub is submerged and ~99% of the sub is above water.
This answer is incorrect, and is intuitively wrong as I don't think a 200,000 kg 2m^3 block would float.
Thanks in advance for your help