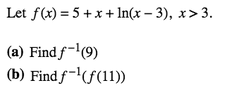Umar
- 36
- 0
Hello, I'm having trouble going about dealing with this question. It asked to find the inverse of the function and evaluate it at a certain number:
View attachment 5963
Also for part b, do we just plug in x=11 and then take the inverse of that output value or what?
I tried using some inverse properties:
f^-1(x) = 9, then, f(x) = 9.
So I set the function equal to 9 and tried to solve for x, but it didn't really work out to well.
Your help is greatly appreciated.
View attachment 5963
Also for part b, do we just plug in x=11 and then take the inverse of that output value or what?
I tried using some inverse properties:
f^-1(x) = 9, then, f(x) = 9.
So I set the function equal to 9 and tried to solve for x, but it didn't really work out to well.
Your help is greatly appreciated.