Solving Centrifugal Forces in a Rotating Coordinate System

[warhammer]

Homework Statement

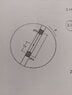
A disk rotates with constant angular velocity ω. Two masses A & B slide without friction in a groove passing through center of disk. They are connected by string of length 'l' and are initially held in position by catch with mass A at a distance r(A) from the center. Neglect gravity. At t=0 the catch is removed and masses are free to slide. Find r''(A) immediately after catch is removed in terms of A,B,l,r(A) & ω.

Relevant Equations

F(A)-T=m(A)*r''(A)

T-F(B)=m(B)*r''(B)

r(A)+r(B)=l

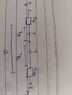
I am also attaching picture of the figure as well as my diagram to showcase the forces.

I have devised these equations because as per the question, r(A) is acting like a reference.

The constraint r(A)+r(B)=l--------(i) transforms to r''(B)= - r''(A) ------- (ii)

Using-

F(A)-T=m(A)*r''(A)

T-F(B)=m(B)*r''(B)

Adding both & using (i) & (ii), F(A)-F(B)= r''(A) {m(A)-m(B)}

r(A)*ω^2 [m(A)+m(B)] - m(B)*l*ω^2= r''(A) {m(A)-m(B)}

{ r(A)*ω^2 [m(A)+m(B)] - m(B)*l*ω^2} /{m(A)-m(B)}

This answer is not coming out to be correct. I sense I have taken force directions wrong but unable to understand why.

 

[haruspex]

T-F(B)=m(B)*r''(B)

Can you see the sign error there?

 

[warhammer]

Can you see the sign error there?

I used this sign convention because r(A) would increase if A tended to move away from the center. Since I used that as reference, I also applied the similar convention for B, T is 'towards' A and F(B) away from it. Can I not do that?

 

[haruspex]

I used this sign convention because r(A) would increase if A tended to move away from the center. Since I used that as reference, I also applied the similar convention for B, T is 'towards' A and F(B) away from it. Can I not do that?

But elsewhere you used r(B) for B's distance from the centre. The tension tends to reduce that and the centrifugal force to increase it.

 

[warhammer]

But elsewhere you used r(B) for B's distance from the centre. The tension tends to reduce that and the centrifugal force to increase it.

I replaced it with (l-r(A)) and r''(A).

(I'm sorry if my questions seem silly sir. It's all new to me and I've hit an understanding block).

 

[Steve4Physics]

EDIT: Changed answer to reflect working in the rotating coordinate system.

Looks like F(A) and F(B) are the (fictitious) centrifugal forces. So you are working in the non-inertial rotating frame-of-reference of the disc.

The usual sign-convention for these radially symmetric problems is 'radially outwards is positive'.

Using this sign convention:
F(A) - T = m(A)*r''(A) is fine because F(A) is outwards and T in inwards
So you need to address the equation T - F(B) = m(B)*r''(B).

 

[warhammer]

EDIT: Changed answer to reflect working in the rotating coordinate system.

Looks like F(A) and F(B) are the (fictitious) centrifugal forces. So you are working in the non-inertial rotating frame-of-reference of the disc.

The usual sign-convention for these radially symmetric problems is 'radially outwards is positive'.

Using this sign convention:
F(A) - T = m(A)*r''(A) is fine because F(A) is outwards and T in inwards
So you need to address the equation T - F(B) = m(B)*r''(B).

Thank you so much for your help sir.