To find the forces acting in a system in equilibrium

[gnits]

Homework Statement

To find the forces acting in a system in equilibrium

Relevant Equations

moments

Could I please ask where I have gone wrong with my reasoning in the following question:

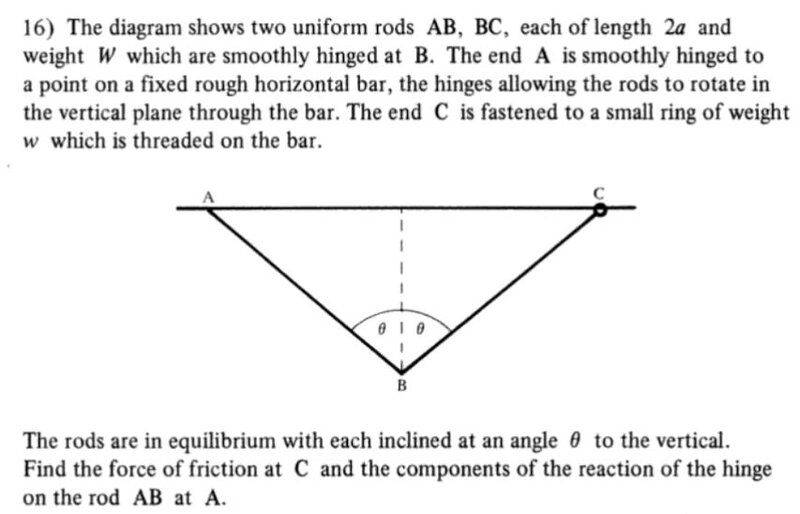
The answers in given in the book are:

(1/2)W tan(Ө)
W vertically
(1/2)W tan(Ө) horizontally

Here is my diagram:

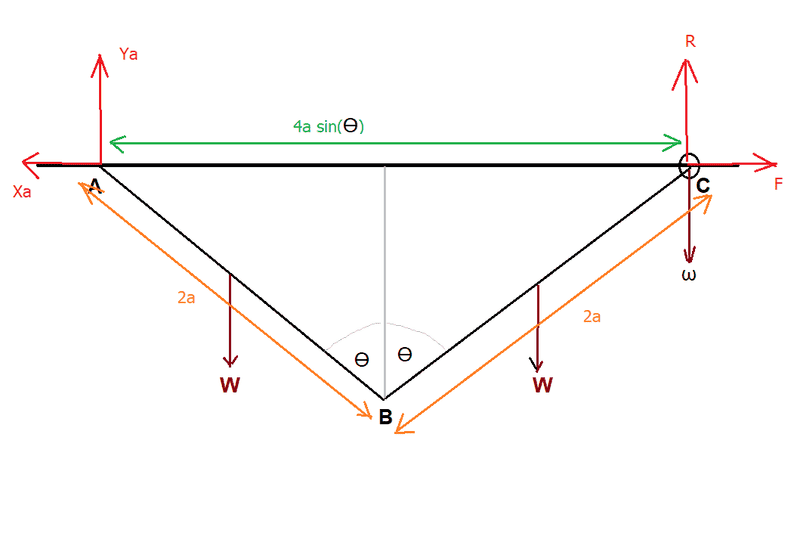
Considering the system as a whole:

(In the text below "Ya" and "Xa" are the forces at the hinge at A)

Resolving vertically gives:

Ya + R = 2W + ω (call this "equation 1")

Resolving horizontally gives:

F = Xa (this agrees with the book answer)

Taking moments about C gives:

W * a sin(Ө) + W * 3a * sin(Ө) = Ya * 4a * sin(Ө)

which gives:

Ya = W (this agrees with the book answer)

And so from "equation 1" we have that R = W + ω (call this "equation 2")

Now, considering the ring alone and taking moments about B gives:

R * 2a * sin(Ө) = ω * 2a * sin(Ө) + F * 2a * cos(Ө)

which gives:

R * tan(Ө) = ω * tan(Ө) + F

So using "equation 2" gives:

F = W * tan(Ө)

But book answer is F = (1/2) * W * tan(Ө)

Where have I reasoned wrongly?

Thanks for any help.

 

[Steve4Physics]

Now, considering the ring alone and taking moments about B gives:

R * 2a * sin(Ө) = ω * 2a * sin(Ө) + F * 2a * cos(Ө)

You have forgotten the moment (torque) produced by BC's weight.

 

[gnits]

You have forgotten the moment (torque) produced by BC's weight.

Thanks very much for that. Indeed, if I include the torque produced by BC's weight everything works out.

This torque is given by W * a sin(Ө)


I guess I am having trouble justifying to myself, why, when I am considering forces on the ring only, I need to include W due to the weight of BC in this way. If I imagine a diagram with the ring only then, if anything, I would label the force on the ring due to BC as being an arrow pointing vertically downwards from the ring of magnitude W. But then it's moment about B would be be

W * 2a * sin(Ө)

not W * a * sin(Ө) as I use above to get the right answer?

How am I thinking of this wrongly?

*EDIT* I think that my confusion is one of visualization. I think that, "mentally", I should be thinking in terms of considering "the rod BC and the ring" as the entity which I am considering in isolation, rather than just "the ring", then indeed I would use W * a sin(Ө)

 

[Lnewqban]

You have a mechanism that would tend to relocate itself to the point of lowest potential energy, where bars AB and BC would become both vertical if nothing would be holding ring C in its position.
AB would simply rotate, while BC must rotate and move, while following the circular trajectory of point B on one end and a horizontal trajectory on the other end.

 

[gnits]

Thanks all for the replies. They have helped me to solve to problem.

 

[Lnewqban]

Thanks all for the replies. They have helped me to solve to problem.

As the angle between the bars increases, the magnitude of the horizontal reaction at pivot A and the necessary friction force at ring C dramatically increases.
At 180 degrees, the value of those forces will be infinite.

Please, see this practical application of this principle of increasing mechanical advantage:
https://roperescuetraining.com/physics_angles.php

You are welcome. :)