No One Has Been Able to Answer This

[Roger Thomas]

Recently, the following math problem was posed to me:

http://www.notobaccoads.com/Images/Math_FindTheArea.jpg

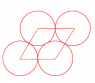
What that chicken scratch above shows is a problem I have not yet been able to solve. By what formula can one determine the area of the space in between three circles of the exact same size touching each other in the arrangement shown above?

The area in the middle isn't a straight edged triangle, it's a three sided space with each side having a curve that somehow relates to the diameter of each circle, I think.

If anyone has any thoughts on how to create a formula to solve for the middle area given any diameter for the three circles or if anyone could point me in the right direction I would appreciate it.

 

[HowardVAgnew]

The area would vary, of course, with the identical diameters of the circles. Trying to dig down into my rusty brain (I won't pretend any of this is from the top of my head), I would think one solution would be to draw an equilateral triangle between the centerpoints of the circles, compute the area of that triangle (call this result X), compute the area of each wedge (I believe they should be identical) formed by the two radii of the triangle intersecting the perimeter of each circle (call this Y). Someone stop me if I am mistaken here, but the points of contact between the circles (I assume they are intended to each have a radius that exactly contacts the other two circles at a single point) should lie on the triangle's laterals. If I am right on that, then I think the area specified would be X - 3Y.

 

[chiro]

Hey Roger Thomas and welcome to the forums.

A quick google search gave this:

http://math.stackexchange.com/questions/49787/area-between-three-circles-of-differing-radii

which allows you to solve for circles with different radii.

 

[Bacle2]

Maybe you can you use integration--restricting the graph of the circle--to find the area between the graphs.

Then, choosing coordinates carefully, say the radius is r. Then center two circles at (r,0) and (-r,0), and the top circle would be centered at (0,2r), find the points of intersection.

I think that should work.

 

[vkash]

I have an idea to do this.(I assume that all the circles are of same radii)
first draw tangents at all the common points between the circles.By symmetry three tangents will cut in between the space between three circles and angle between three tangents will be 120 degrees(do you got it?).
Now area of space between three circles is =3(area_of_quadrilateral_formed_tangents_to_a_circle_and_corresponding_radii-1/6area_of_a_circle)
Do you understood how i write last line??

I doesn't understand what you write in right part of image...
see attachment i have edited and drawn tangents
for different radii see the link given by chiro. that requires knowledge trigonometry.
why go for integration and other lengthy processes if it can be quite easy done with simple geometry..

 

[DaveC426913]

This can be solved pretty trivially. About 2 lines.

The trick is to rearrange it into areas much easier to calculate. By tiling.

Here is a big hint.

 

[vkash]

This can be solved pretty trivially. About 2 lines.

The trick is to rearrange it into areas much easier to calculate. By tiling.

Here is a big hint.

it is also valid only for similar circles else it became to tricky to find out the area of quadiletral as well as of circles. am i correct DaveC426913

 

[altamashghazi]

the triangle formed by joining the centres of circle is equilateral with side 2r. area of this is
√3/4*(2r)^2. now area of the three sectors is 3(πr^2/2).
required area is subtraction of the above two.

 

[DaveC426913]

it is also valid only for similar circles else it became to tricky to find out the area of quadiletral as well as of circles. am i correct DaveC426913

The OP did specify that all circles are the same size.

 

[DaveC426913]

the triangle formed by joining the centres of circle is equilateral with side 2r. area of this is
√3/4*(2r)^2. now area of the three sectors is 3(πr^2/2).
required area is subtraction of the above two.

Heh. Exactly the same as my answer except I doubled it.

 

[altamashghazi]

if it is done so simply then why double it and make it more calculative.

 

[Dadface]

the triangle formed by joining the centres of circle is equilateral with side 2r. area of this is
√3/4*(2r)^2. now area of the three sectors is 3(πr^2/2).
required area is subtraction of the above two.

When you wrote 3nr^2/2 did you mean nr^2/2?

 

[Mentallic]

When you wrote 3nr^2/2 did you mean nr^2/2?

Yes, it should have been 3(\pi r^2/6)

 

[DaveC426913]

if it is done so simply then why double it and make it more calculative.

Yep. Yours is better.

 

[altamashghazi]

yes it was mistakely written. i meant πr^2/2. mentallic is correct.

 

[dijkarte]

I have an answer for circles with different radii. :)

 

[Mentallic]

I have an answer for circles with different radii. :)

Care to share it?

 

[dijkarte]

The idea is to form a triangle whose vertices are the circles' center points. Calculate the area of the triangle and subtract the sector/pie area of each circle.

Assume the circles have radii of r1, r2, and r3.

You can position one circle at the origin p1(0, 0), the second will be at p1(r1 + r2, 0) and the trick is to find the position of the third circle p3(a, b) which is left as exercise. Now using the three positions, you can use the vectors [p1, p2], [p1, p3], ... to calculate the angles of each sector, which is then used to calculate the area of the sector.