Normal contact force with angles

[furor celtica]

Homework Statement

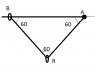
A small smooth ring R, of mass 0.6 kg, is threaded on a light inextensible string. One end of the string is attached to the fixed point A and the other end is attached to a ring B, of mass 0.2 kg, which is threaded on a fixed rough horizontal wire which passes through A (see diagram (excuse the obviously unequal angles)). The system is in equilibrium, with B about to slip and with the part AR of the string making an angle of 60° to the wire.
a. Explain, with reference to the fact that ring R is smooth, why the part BR of the string is inclined at 60° to the wire.
b. Show that the normal contact force between B and the wire has magnitude 5 N.
c. Find the coefficient of friction between B and the wire.

Homework Equations

The Attempt at a Solution

For a. I was unsure of what wording to use exactly, and answered the following:
a. Ring R being smooth and ring B being on the same horizontal plane as fixed point A, ring R will have slipped to the midpoint of the string: angles ABR and RAB are therefore equal.
Angle RAB being given as 60°, this means that the part BR of the string is inclined at 60° to the wire.

For b. however I have several problems. Firstly, of how the 6N weight of R is distributed over both string segments (RB and AR). I would assume that the each segment carries half the load, but I’m unsure of how to prove this. Secondly, even taking 3cos30 N (half of R’s weight resolved for the slope of the string) as the tension in the string segment BR, I end up with normal contact force = 2 (weight of B) + 3cos30(cos30) = 4.25 N

Any suggestions?

 

[NascentOxygen]

The tension in the string is uniform throughout its length. (This would not be true were something to be 'tied' to the string, rather than being free to slide.)

a. At R, the horizontal component of the tension to the right is exactly balanced by the horizontal component to the left, since R contributes no horizontal force (because the string has zero coeff of friction). As the tension in the string is uniform, for the horiz components of force to exactly balance the angles to the horizontal of the string as it passes around R must be equal. The system is in static equilibrium, so at this point the two vertical components due to tension must balance the weight of R. So now you can calculate the tension in the string.

b. At B, you have the weight of B added to the vertical component of the string's tension. Friction contributes only a horiz component.

 

[rl.bhat]

If T is the tension in the AR an BR , then 6 N = 2*T*cos(30)
So T = 3/co(30) N
Vertical component of T is T*cos(30)
Now proceed.