Normalised Radial Coulomb Wave Function

[tomdodd4598]

Hey there,

I used Mathematica to find the (non-normalised) wave function of an electron in the vicinity of a Hydrogen nucleus, and converted the answer from one involving Whittaker functions to one involving generalised Laguerre polynomials. My result is shown below:

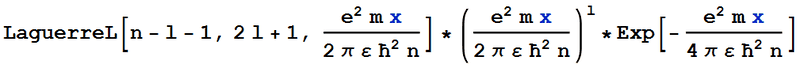
This agrees with the documented non-normalised wave function. However, when I multiply by the documented normalisation constant, to get the following wave function:

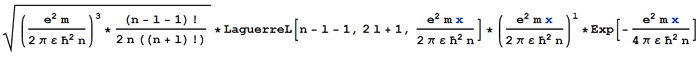
It is still not normalised - the integral from 0 to infinity of the absolute square is still not equal to 1.

Does anyone know what I'm doing wrong, and/or how to fix the wave function? Thanks in advance.

 

[dextercioby]

Which reference did you take for the unnormalized bound-state wavefunction?

 

[tomdodd4598]

Which reference did you take for the unnormalized bound-state wavefunction?

This is the page where I found the function with a Laguerre polynomial (I've rearranged a few terms and added the constants, but otherwise it's the same): http://ampl.github.io/amplgsl/coulomb.html

I think I know where I'm going wrong, however. It seems that the function is only normalised once this radial part is multiplied by the angular part. I guess I could find the angular part, but I was wandering whether there was a way to just normalise this function on its own, so that I can calculate the probability of finding an electron however far from the nucleus, without worrying about the angular coordinates.

 

[dextercioby]

Of course you can find a constant only from the normalization of the radial part alone, but it's not the one you for the probabilistic interpretation. The unnormalized radial distribution can be used to graph it (critical points, inflection, zeros), but the probability is gotten only from the full wavefunction (which includes the angular part and its own normalization constant).

 

[tomdodd4598]

Of course you can find a constant only from the normalization of the radial part alone, but it's not the one you for the probabilistic interpretation. The unnormalized radial distribution can be used to graph it (critical points, inflection, zeros), but the probability is gotten only from the full wavefunction (which includes the angular part and its own normalization constant).

Ah, ok. So if I find the angular function(s), could I integrate the absolute square of the whole wave function over θ from 0 to 2π, over ϕ from -π/2 to π/2, then between two values of radius to find the probability of finding the electron between those radii?

 

[dextercioby]

It's actually in a spherical shell of finite width, because, by the way you've chosen them, the 2 angles vary maximally therefore covering a whole sphere.