- #1
lishrimp
- 2
- 0
Hi.
I have a few simple questions.
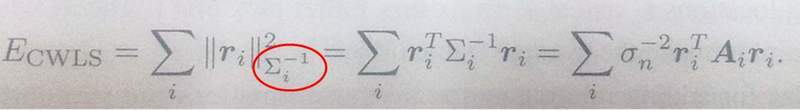 (<- sorry, please click this image.)
(<- sorry, please click this image.)
1. What does the notation in the red circle mean?
2. Is there a rule for expanding square of norm? (e.g. || A*B*C ||^2)
I don't really understand how the first eq. changes to the second eq.
Thanks. :)
I have a few simple questions.
1. What does the notation in the red circle mean?
2. Is there a rule for expanding square of norm? (e.g. || A*B*C ||^2)
I don't really understand how the first eq. changes to the second eq.
Thanks. :)