TylerH
- 729
- 0
Notation "(v*gradient operator)v" in Navier-Stokes
What does \left( \textbf{v} \cdot \nabla \right) \textbf{v} mean, assuming knowledge of the gradient operator? And, specifically, how would that be expanded? In general, I'm ignorant of the notation \left( f \left( y, \frac{d}{dx}, \frac{d^2}{dx^2}, \ldots \right) y \right) where, for example, f \left( y, \frac{d}{dx}, \frac{d^2}{dx^2}, \ldots \right) could be y + \frac{d}{dx}.
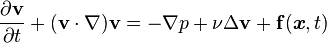
What does \left( \textbf{v} \cdot \nabla \right) \textbf{v} mean, assuming knowledge of the gradient operator? And, specifically, how would that be expanded? In general, I'm ignorant of the notation \left( f \left( y, \frac{d}{dx}, \frac{d^2}{dx^2}, \ldots \right) y \right) where, for example, f \left( y, \frac{d}{dx}, \frac{d^2}{dx^2}, \ldots \right) could be y + \frac{d}{dx}.