Number of lines equidistant from four points on a plane

[mahblah]

Homework Statement

Four points in the plane are given, not all on the same straight line, and not all on a circle. How many straight lines and circles can be drawn which are equidistant from these points?

Relevant Equations

by distance from a point P to a circle c with center O we mean the lenght of the segment PQ, where Q is the point where the ray from O in the direction OP meets c

Hi, i'm trying to solve this problem.

It's exercise 3 on page 5 from this book:
Challenging mathematical problem with elementary solutions

The solution is on page 41:

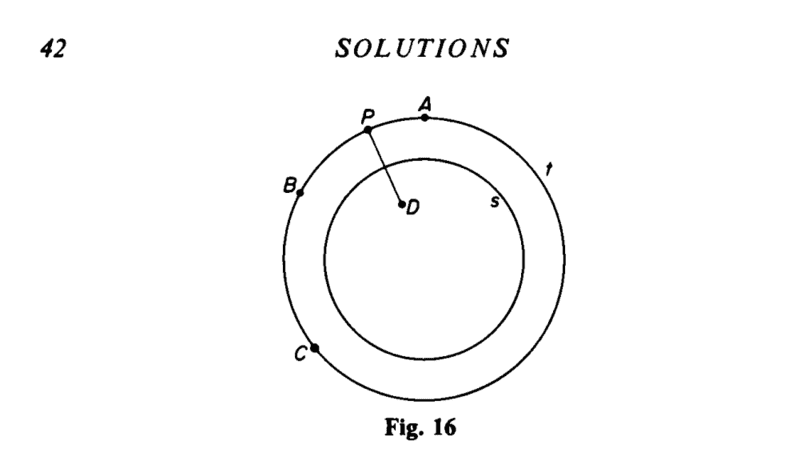
I'm OK with the 4 circles in case 1: i can pick (inside/outside):
ABC + D,
ABD + C,
ADC + B,
BCD + A.
What i cannot understand is how there can be 4 straight lines in case 1:
if three points stand on one side of the equidistant line, these point must be collinear, and so there is only one possible straight line (i cannot re-arrange them!)

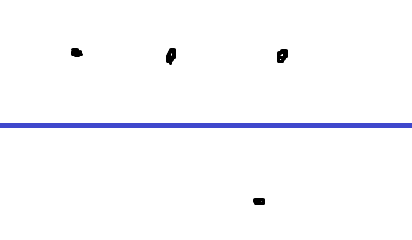
where am I wrong?

thanks

 

[DrClaude]

The phrasing of the answer lead to a misunderstanding. It is never four straight lines, it is either four circles or three circles and a straight line. If A, B, and C are collinear, then you can draw a straight line as you did, and three circles concentric with the circles passing through ABD, ACD, and BCD.

 

[mahblah]

Oh that makes sense
Thanks!