- #1
QFT1995
- 30
- 1
If I have a Lagrangian of the form
[tex]\mathcal{L}=-\frac{1}{2} (\partial \phi)^2 - \frac{1}{2} m^2 \phi^2 - \frac{\lambda}{3!} \phi^6, [/tex]
in 3 dimensions, what is the one-loop correction to the 4-point function? Am I correct in thinking that the following Feynman diagram is the representation of the 4 point function for this Lagrangian?

The only one-loop diagram I can think of is
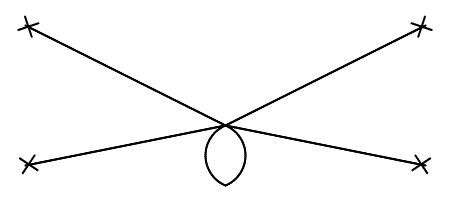
however I'm struggling to see how this is explicitly a correction to the 4 point function I drew above.
[tex]\mathcal{L}=-\frac{1}{2} (\partial \phi)^2 - \frac{1}{2} m^2 \phi^2 - \frac{\lambda}{3!} \phi^6, [/tex]
in 3 dimensions, what is the one-loop correction to the 4-point function? Am I correct in thinking that the following Feynman diagram is the representation of the 4 point function for this Lagrangian?
The only one-loop diagram I can think of is
however I'm struggling to see how this is explicitly a correction to the 4 point function I drew above.