A One Loop Correction to a 4 pt. function in 3 dimensions

[QFT1995]

If I have a Lagrangian of the form
\mathcal{L}=-\frac{1}{2} (\partial \phi)^2 - \frac{1}{2} m^2 \phi^2 - \frac{\lambda}{3!} \phi^6,
in 3 dimensions, what is the one-loop correction to the 4-point function? Am I correct in thinking that the following Feynman diagram is the representation of the 4 point function for this Lagrangian?

The only one-loop diagram I can think of is

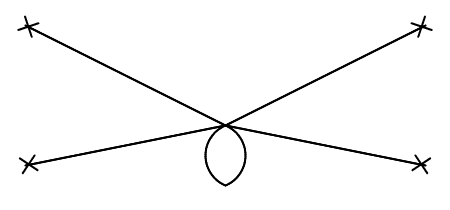
however I'm struggling to see how this is explicitly a correction to the 4 point function I drew above.

 

[vanhees71]

It's a bit unusual to consider disconnected diagrams (the first one you've drawn). For the connected diagrams the 2nd diagram is the leading-order contribution to the four-point function.

Since you Lagrangian has no $\phi^4$ term, at this point you'd have to introduce one, because this loop is (in 3D linearly) divergent and thus you need a $\phi^4$-term in the Lagrangian to renormalize it.

 

[QFT1995]

Hi, this was an question from a problem set where there was no \phi^4 term. The question later asks whether the theory is renormalizable or not. When talking about one-loop order corrections, are the corrections always to the connected diagrams and not the disconnected ones?

 

[vanhees71]

For renormalization you only need to consider the even smaller subset of the one-particle irreducible connected amputated diagrams (the proper vertex functions).

To see whether $\phi^6$ theory is (Dyson-)renormalizable in $d$ spacetime dimensions we have to evaluate the "superficial degree of divergence". To that end note that any vertex simply provides just a constant, and any propagator with momentum $p$ goes like $1/p^2$ in the UV. Any loop adds integration over the corresponding loop momentum providing an integration over the momentum. Thus the superficial degree of divergence is
$$D_s=L d-2I,$$
where $L$ is the number of loops and $I$ the number of internal lines of the diagram.

Now consider a diagram with $V$ vertices (i.e., of order $V$ of perturbation theory) and $E$ external lines. At each vertex momentum conservation holds, i.e., the sum of all momenta running into or out of the vertex must be 0. Thus we have for the number of loops
$$L=I-V+1,$$
since only internal lines provide momenta over which we may have to integrate. At each vertex one momentum is fixed due to momentum conservation, but there's one overall conservation for all external momenta which doesn't constrain the independent momenta on internal lines.

Finally into each vertex run 6 lines. Each internal line connects two vertices, while the external lines don't count as internal lines by definition, thus we have
$$I=(6V-E)/2.$$
Note that in $\phi^6$ theory all proper vertex functions with an odd number of external lines vanish due to the symmetry of the theory under the "field reflection" $\phi \rightarrow -\phi$, i.e., we have to consider only an even number for $E$, and thus $I$ is always an integer number as it must be.

Now we can combine the three equations above:
$$D_s=d+\frac{2-d}{2} E +(2d-6)V.$$
For $d=3$ this gives
$$D_s=3-\frac{E}{2}.$$
Thus $D_s \geq 0$ for $E \in \{0,2,4,6 \}$ only and this means the theory is superficially renormalizable. Since there are no further symmetries providing Ward-Takahashi identities due to the BPHZ analysis the theory is thus (Dyson-)renormalizable, provided there's also a four-point vertex, such that the divergence of the four-point functions can be absorbed into the four-point coupling constant.

 

[QFT1995]

Thank you for your help. Can you tell me if this is correct or not. Is the one loop diagram I drew above finite since
\int \frac{d^d k}{(2\pi)^d} \frac{1}{k^2 +m^2 -\imath \epsilon} \propto \Gamma\left(1-\frac{d}{2}\right)
is finite for d=3?

Edit: I just re-read your reply above saying that this integral should be linearly divergent so I don't know where I've gone wrong.

 

[vanhees71]

Let's calculate the Euclidean (Wick rotated) integral. Then with a cut-off $|k|<\Lambda$
$$\int_{K_{\Lambda}} \frac{\mathrm{d}^3 k}{(2 \pi)^3}\frac{1}{k^2+m^2} = \frac{1}{2 \pi^2}\int_0^{\Lambda} \mathrm{d} k \frac{k^2}{k^2+m^2} = \Lambda - m \arctan(\Lambda/m),$$
and this diverges linearly with the cutoff as expected.