One vertex interactions in QED - error in the book?

[Wrichik Basu]

I am studying QFT from the book A First Book of QFT. I am currently in the chapter of QED.

The authors have written down the interaction Lagrangian for QED. Thereafter, they have taken a special case of the electron, and written down the normal-ordered interaction Hamiltonian for this case: $$:\mathcal{H}_{\text{int}}: \ = \ -e:\bar{\psi} \gamma ^\mu \psi A_\mu:,$$ where $\psi$ and $\bar{\psi}$ are the free Dirac field operators, one for the particle and the other for the anit-particle, and $A_\mu$ is the operator of the free EM field.

Then the authors have decomposed each field operator in terms of their creation and annihilation parts, like $\psi \ = \ \psi_+\ + \ \psi_-$ where $\psi_+$ has the annihilation part, and $\psi_-$ has the creation part. Same goes for the other two operators.

If we write each field operator in terms of their creation and annihilation sub-parts, the interaction Hamiltonian has 8 terms. The authors have then said:

As you can see, thay have taken $\bar{\psi}$ for the positron and $\psi$ for the electron. Well and good, I have understood everything so far.

Soon after this, they have written,

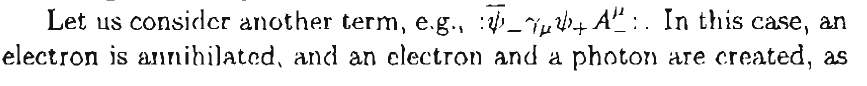
How can this be correct? If I follow the previous arguments, $\psi_+$ annihilates an electron, $\bar{\psi}_-$ creates a positron, not an electron, and $A^\mu_-$ creates a photon.

The corresponding Feynman diagram is:

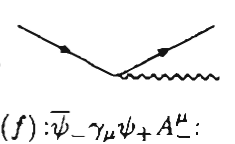
Thereafter they have proceeded to show how none of the eight terms can represent physical processes if all particles are considered on-shell. But nothing about this has been mentioned elsewhere.

I checked out the errata of the book, but they have not written anything about this. Am I correct and the book is wrong, or am I missing something?

 

[A. Neumaier]

The book is right. The diagram represents an interaction of virtual particles only, which are not physical and hence can be off shell.

 

[Wrichik Basu]

The book is right. The diagram represents an interaction of virtual particles only, which are not physical and hence can be off shell.

I understood that they can be off-shell. But tell me one thing: following the arguments of the authors, they first took $\psi$ for the electron and $\bar{\psi}$ for the positron, but soon after that, they took the reverse, that is, $\psi$ for the positron and $\bar{\psi}$ for the electron. Is this change correct because the particles are virtual?

 

[vanhees71]

The field operator $\psi$ is made up of annihilation operators for electrons (in front of the positive-frequency modes) and a creation operator for positrons (in front of the negative-frequence modes). Since annihilation and creation operators are adjoint to each other this implies that $\bar{\psi} = \psi^{\dagger} \gamma^0$ it's the other way: $\bar{\psi}$ consists of a creation operator for electrons and an annihilation operator for positrons.

This (and only this!) specific structure of the field operator makes a local realization of the proper orthochronous Poincare group and leads to a Hamilton density fulfilling the microcausality constraint. Together with the demand to have an energy spectrum that is bounded from below, you have to quantize the field as fermions (spin-statistics theorem).

Now the author splits the field operators (analogously for photons, only that there particle and antiparticle are identical and of course bosons) and analyzes the various combinations occurring in the elementary QED vertex. As far as I can see from what you've quoted this is all correct, but you must take it with a grain of salt. Since this elementary vertex doesn't depict any matrix elements of physical processes since all these formal processes given by the split of the field operators are forbidden due to energy-momentum conservation. This means the vertex is just a mathematical notation for the perturbative expansion but nothing directly physical. You can of course build Feynman diagrams from these building blocks which describe physical processes. There the external legs refer to the mode functions, the inner lines to Feynman (in the vacuum QFT we are discussing here identical with the time-ordered) propagators. The vertices stand for $\mathrm{i} e \gamma^{\mu}$. If a process is allowed by all conservation laws you get S-matrix elements and cross sections from the formalism (in the perturbative approximation to an order in $\alpha_{\text{em}}$ given by the number of vertices in the diagram).

 

[Wrichik Basu]

The field operator ψψ\psi is made up of annihilation operators for electrons (in front of the positive-frequency modes) and a creation operator for positrons (in front of the negative-frequence modes).

Yes yes, I just missed that somehow. Thanks.