mcastillo356
Gold Member
- 643
- 351
- TL;DR
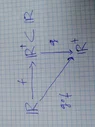
- I'm almost sure, but need to check it with the forum. It's about the first chapter of "Introduction to topology and modern analysis" I am reading online.
The textbook is being fine. I asked the forum for some introduction to topology, and decided to start with Simmon`s. This naive question is due to ignorance of the words into and onto, which I don't distinguish in Spanish. A quick browsing sugests I'm right.