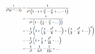Video (analytic continuation) seems to mix 4-D & 2-D maps

[nomadreid]

The question here is not asking for links to help understand analytic continuation or the Riemann hypothesis, but rather help in understand the bits of hand-waving in the following video’s explanations : https://www.youtube.com/watch?v=sD0NjbwqlYw (apparently narrated by the same person who does Khan Academy videos), an introduction to the Riemann hypothesis at a pre-calculus level.(But the answers do not need to be at that level.)

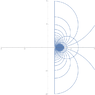
[1] At 9:56 he somehow reduces the 4-dimensional map of the zeta function on {s ∈ ℂ: Re(s) >1} to a two dimensional map. (It seems he is including the whole map, not just the set of values, not just from his drawings but also because in his example of a simpler 4-D map, starting at 8:53, he says that “it all happens in two dimensions” at 9:20.) So my first question: what family of curves is he referring to?

[2] Then, at 13:13, he goes back to the idea of the four-dimensional map, and says that the zeta function, being analytic (except at the pole), is then conformal except at the points where the derivative vanishes, where (at 14:19) he says that the angles get multiplied by an integer n. Then, at 14:22 he says that the points of vanishing derivative are “by far the minority”. Several questions based on this:

(a) As the number of continuous curves in C is that of the continuum, is he saying that the points of vanishing derivative is countable (not to get nitpicky with whether or not one assumes the continuum hypothesis)?

(b) is there a way to determine that integer n?

(c) At 15:46 he again goes back to representing the zeta function as a four-dimensional map, he says that to keep the continuation of an analytic function analytic “that is, that it still preserves angles everywhere” – presuming that the viewer remembers the caveat about the points of vanishing derivative. But if there is a way to determine n in (b), would it have been valid to make the caveat explicit by saying “that it still preserves angles everywhere at the points of non-zero derivative and that multiplies the angle by n otherwise.” ? Could the caveat be made simpler somehow with the concept of continuity instead?

Thanks.

 

[aheight]

[1] At 9:56 he somehow reduces the 4-dimensional map of the zeta function on {s ∈ ℂ: Re(s) >1} to a two dimensional map. (It seems he is including the whole map, not just the set of values, not just from his drawings but also because in his example of a simpler 4-D map, starting at 8:53, he says that “it all happens in two dimensions” at 9:20.) So my first question: what family of curves is he referring to?
Thanks.

There is some confusion in the video: the Euler sum is not the zeta function. Rather, Riemann, in his effort to compute a formula for the number of primes under a given number, analytically continued the sum beyond it domain of convergence, that is, to all the z-plane. That function is in my opinion one of the most beautiful constructs in mathematics:

$$\zeta(s)=\frac{\Gamma(1-s)}{2\pi i} \mathop\int_{\multimap} \frac{s^{t-1}}{e^{-t}-1}dt$$

If that integral doesn't get you to love Complex Analysis, you have no heart!

The contours the narrator is referring is the actual mapping of the function or in the case of Re(z)>1, of the Euler sum. Just start simple: take the line s=x+i from say x=1.1 to x=10. Compute what u=$\zeta(s)$ is for a set of points in that range say 30 or so points. Now plot in the u-plane (Re(u),Im(u)) and connect the points. That is one contour. Now do this for a bunch of horizontal and vertical lines in the z-plane for Re(z)>1 and you will get those contours (in the u-plane) shown in the video. Now in order to get the remaining parts of the picture for Re(z)<1, you would have to use one of the expressions for the analytic-continuation of the sum into the domain Re(z)<1 (since the Euler sum doesn't converge in that region) and with some effort, you can even numerically compute the contour integral expression above to do it. If you check a bit, there is an infinite sum expression for the function that converges for Re(z)<1 except at the pole of the function (I think).

 

[nomadreid]

Thanks very much, aheight. That makes sense. I was not looking at it from the point of view of a contour integral. (I am very weak in that area, so I must delve more into contour integral techniques.) So in essence this is not the graph of the whole (4D) function, but rather the graph of (a selection of) its values (i.e., a subset of the codomain), hence 2D.

If you check a bit, there is an infinite sum expression for the function that converges for Re(z)<1 except at the pole of the function (I think).

Apparently, yes, according to https://math.stackexchange.com/questions/728590/calculation-of-a-residue: (being very slow with LaTex, I will take the coward's way out and just paste the derivation)

although I am not sure whether there is a shorter way to go from the third line to the fourth line besides laboriously calculating the Cauchy product each time.

So this answers my main question in [1]. If I am lucky someone will also turn their attention to [2].

 

[aheight]

Thanks very much, aheight. That makes sense. I was not looking at it from the point of view of a contour integral. (I am very weak in that area, so I must delve more into contour integral techniques.) So in essence this is not the graph of the whole (4D) function, but rather the graph of (a selection of) its values (i.e., a subset of the codomain), hence 2D.


Apparently, yes, according to https://math.stackexchange.com/questions/728590/calculation-of-a-residue: (being very slow with LaTex, I will take the coward's way out and just paste the derivation)
View attachment 223981
although I am not sure whether there is a shorter way to go from the third line to the fourth line besides laboriously calculating the Cauchy product each time.

So this answers my main question in [1]. If I am lucky someone will also turn their attention to [2].

Don't worry about the contour integral, I just posted it because it's beautiful. Basically, we are just mapping horizontal and vertical lines in the z-plane using the zeta function into the u-plane. Mathematica is very helpful to do this numerically if you have it. There is a zeta function built-into it.

 

[aheight]

Here is a quick Mathematica plot in the u-plane of a horizontal and vertical grid over the z plane mapped by u=$\zeta(z)$. Notice how I plot in the u-plane, the coordinates {Re[zeta(z)],Im[zeta(z)]}. The plot is a bit rough but we can begin to see the similarity to the plots in the video.

myHorizContours =  Table[ParametricPlot[{Re[Zeta[z]], Im[Zeta[z]]} /. z -> x + I y, {x,
      1, 10}, PlotRange -> 2], {y, -10, 10, .125}];
myVertContours =  Table[ParametricPlot[{Re[Zeta[z]], Im[Zeta[z]]} /.
     z -> x + I y, {y, -10, 10}, PlotRange -> 2], {x, 1, 10, 0.5}];
Show[{myHorizContours, myVertContours}, PlotRange -> 4]

 

[nomadreid]

Super! This supports your previous answer very well. Thanks again, aheight.

 

[nomadreid]

One little detail: I know you told me to forget about the contour integral, but I do think that this is a good opportunity for me to fill in this hole in my mathematics. So, I noticed a slight discrepancy between the version you posted and the one given in http://mathworld.wolfram.com/RiemannZetaFunction.html, where the contour integral is almost the same as yours, but with the difference (translating into your notation, z→s & u→t) that you have in the argument of the integral s^t-1 as opposed to mathworld's t^s-1. Is this a typo on someone's part, or am I missing something?

PS I just noticed that my post #3 only had the expansion for the case "variable in the exponent of the numerator"=-1. Oops. Back to the drawing board.

 

[aheight]

One little detail: I know you told me to forget about the contour integral, but I do think that this is a good opportunity for me to fill in this hole in my mathematics. So, I noticed a slight discrepancy between the version you posted and the one given in http://mathworld.wolfram.com/RiemannZetaFunction.html, where the contour integral is almost the same as yours, but with the difference (translating into your notation, z→s & u→t) that you have in the argument of the integral s^t-1 as opposed to mathworld's t^s-1. Is this a typo on someone's part, or am I missing something?

PS I just noticed that my post #3 only had the expansion for the case "variable in the exponent of the numerator"=-1. Oops. Back to the drawing board.

Ok thanks. My mistake:

$$\zeta(s)=\frac{\Gamma(1-s)}{2\pi i}\mathop\int_{\multimap} \frac{u^{s-1}}{e^{-u}-1}du $$

And I did mention we can compute the zeta function by numerically-integrating the contour integral. However, it is a bit unstable. Here is the Mathematica code I used to compute $\zeta(-4+i)$. Remember we are in general integrating over a multi-valued function along a Hankel path. And although in the limit, the two horizontal legs of the contour are exactly over the negative real axis, for numerical results, we integrate just below the axis via u=x-delta i, go around the origin via u=re^(it) then just above the axis using u=x+delta i. The two output lines compare the numerical results to the built-in Zeta(z) function in Mathematica.

In[1184]:=
delta = 1/100000000;
s = -4 + I;
r = 1/20;
difa = N[ArcTan[delta/r]];
n3 = NIntegrate[Exp[(s - 1)*(Log[Abs[u]] + I*Arg[u])]/(Exp[-u] - 1) /. u -> x - delta*I, {x, -10000, -r},
    WorkingPrecision -> 160];
n4 = NIntegrate[Exp[(s - 1)*(Log[Abs[u]] + I*Arg[u])]/(Exp[-u] - 1) /. u -> x + delta*I, {x, -r, -10000},
    WorkingPrecision -> 160];
n5 = NIntegrate[(Exp[(s - 1)*(Log[Abs[u]] + I*Arg[u])]/(Exp[-u] - 1))*I*r*Exp[I*t] /. u -> r*Exp[I*t],
    {t, -Pi + difa, Pi - difa}, WorkingPrecision -> 160];
N[Zeta[s]]
N[(Gamma[1 - s]/(2*Pi*I))*(n3 + n4 + n5)]

Out[1191]= -0.00353984 + 0.00975032 I

Out[1192]= -0.00353501 + 0.00975131 I

 

[nomadreid]

Thanks, aheight. As I do not use Mathematica, and have not yet had time to properly learn how to calculate contour integrals, I will in future try to take that program apart and figure out what you did. I am afraid I am not even sure what the arctan is doing there; my first guess that it had something to do with the formula

does not, on second glance, seem to be reasonable. So this is on my list of projects. Thanks for sending me that way.
In the meantime, I don't suppose you have looked at the rest of my original question, that is, part [2]?