Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading "Multidimensional Real Analysis I: Differentiation by J. J. Duistermaat and J. A. C. Kolk ...
I am focused on Chapter 1: Continuity ... ...
I need help with the proof of Lemma 1.2.11 ...
Duistermaat and Kolk"s Lemma 1.2.11 reads as follows:
View attachment 9020
View attachment 9021
Can someone please demonstrate formally and rigorously how we can, by taking complements, obtain Lemma 1.2.11 from Lemma 1.2.4 ...
Help will be appreciated ...
Peter
=====================================================================================The above post mentions Lemma 1.2.4 so I am providing text of the same ... as follows:
View attachment 9022
It may help MHB readers of the above post to have access to Duistermaat and Kolk's definition of open sets so I am providing text of the same ... as follows:View attachment 9023
View attachment 9024... and a closed set is simply a set whose complement is open ... ... Hope that helps ... Peter
I am focused on Chapter 1: Continuity ... ...
I need help with the proof of Lemma 1.2.11 ...
Duistermaat and Kolk"s Lemma 1.2.11 reads as follows:
View attachment 9020
View attachment 9021
Can someone please demonstrate formally and rigorously how we can, by taking complements, obtain Lemma 1.2.11 from Lemma 1.2.4 ...
Help will be appreciated ...
Peter
=====================================================================================The above post mentions Lemma 1.2.4 so I am providing text of the same ... as follows:
View attachment 9022
It may help MHB readers of the above post to have access to Duistermaat and Kolk's definition of open sets so I am providing text of the same ... as follows:View attachment 9023
View attachment 9024... and a closed set is simply a set whose complement is open ... ... Hope that helps ... Peter
Attachments
-
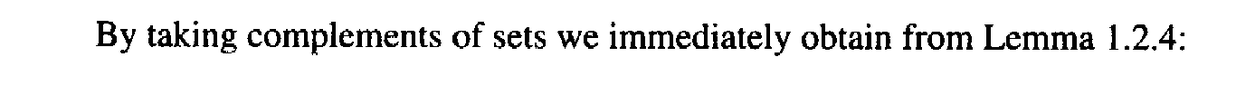 D&K - 1 - Lemma 1.2.11 ... PART 1 ... .png1.8 KB · Views: 162
D&K - 1 - Lemma 1.2.11 ... PART 1 ... .png1.8 KB · Views: 162 -
 D&K - 2 - Lemma 1.2.11 ... PART 2 ... .png2.1 KB · Views: 137
D&K - 2 - Lemma 1.2.11 ... PART 2 ... .png2.1 KB · Views: 137 -
 D&K - Lemma 1.2.4 ... .png13.1 KB · Views: 147
D&K - Lemma 1.2.4 ... .png13.1 KB · Views: 147 -
 D&K - 1 - Start of Section 1.2 ... Open and Closed Sets ... .png5.8 KB · Views: 143
D&K - 1 - Start of Section 1.2 ... Open and Closed Sets ... .png5.8 KB · Views: 143 -
 D&K - 2 - Start of Section 1.2 ... Open and Closed Sets ... ...Part 2.png32.3 KB · Views: 145
D&K - 2 - Start of Section 1.2 ... Open and Closed Sets ... ...Part 2.png32.3 KB · Views: 145
Last edited: