everlasting89
- 3
- 0
Homework Statement
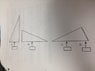
When the striking ray is held perpendicular to the prism, there are four general configurations possible (in the attachment below). Use the figure on the next page to determine analytically which of these four configurations will result in total internal reflection of the light ray. Show analytical work and try each setup. Sketch the results.
Homework Equations
sin θ = (n1 / n2)(sin 90)
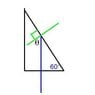
Angles of the prism: 90, 59, and 31 degrees
The Attempt at a Solution
Found the critical angle:
sin θ = (n1 / n2)(sin 90)
sin θ = (1.5/1)(sin 90)
sin θ = (1.5/1)(1)
θ = 41.8 degrees
And I know that for total internal reflection the angle of incidence must be larger than the critical angle. However, I am stuck on what (and how) to do next.
Any help is much appreciated!
Attachments
Last edited: