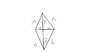Optimizing Kite Area: Solving x,y,z for Max Area

[trajan22]

I have a kite pictured below...i need to determine x y z so that the kite has a maximum area. a and b are fixed constants.

The way I am thinking of trying this is to have this equation
(x*y)+(z*x)=A
from this i have three variables so i should solve for y in terms of x and solve for z in terms of x this will give me one equation one unknown so i can differentiate and set it equal to zero. therefore solving.

Would this be a correct approach for this problem...(sorry about the poor drawing, its difficult on a touchpad)

 

[0rthodontist]

I think you mean xy + zx = area

A and B are fixed constants. You need to make two more equations relating A to x and y, and B to x and z.

 

[trajan22]

so for those other 2 eqs would it be A^2=x^2+Y^2
B^2=x^2+z^2