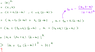Onezimo Cardoso
- 11
- 2
Homework Statement
Given ##a\neq b## vectors of ##\mathbb{R}^n##. Determine ##c## which lies in the line segment ##[a,b]=\{a+t(b-a) ; t \in [0,1]\}##, such that ##c \perp (b-a)##. Conclude that for all ##x \in [a,b]##, with ##x\neq c## it is true that ##|c|<|x|##.
Homework Equations
The first part of the question can be solved just using inner product definition.
I don't know how the second part can be solved. But I think could be useful the Cauchy-Schawarz inequality ##|<x,y>| \leq |x||y|## or maybe the cosine rule...
The Attempt at a Solution
If we suppose that ##c \in [a,b]## then we can write ##c## as:
$$c=a+t_0 (b-a)$$
where ##t_0 \in [0,1]##.
By the fact that ##c \perp (b-a)## we have:
$$<c,(b-a)> \quad = \quad0$$
$$\Rightarrow \quad <a+t_0 (b-a),(b-a)> \quad = \quad 0$$
$$\Rightarrow \quad <a,(b-a)>+<t_0 (b-a),(b-a)> \quad =\quad 0$$
$$\Rightarrow \quad <a,(b-a)>+t_0 |b-a|^2=0$$
$$\Rightarrow t_0 = - \frac{<a,(b-a)>}{|b-a|^2} $$
Then ##c## can be uniquely determined as ##c=a+t_0 (b-a)##, where ##t_0 = - \frac{<a,(b-a)>}{|b-a|^2}##.
$$\ldots$$
Now we need to prove that if we consider any other ##x \neq c## in the line segment ##[a,b]## then ##|c|<|x|##.
Attachments
Last edited: