LCSphysicist
- 644
- 162
- Homework Statement
- Be the set of points (x,y) which "figure one".
And in the semiplane y >= 0.
Show the volume of the solid obtained by rotation about the axis x, of the set A, is equal to the product of the area of the ellipsoid with the circumference generated in the rotation of the center (alpha,beta) of the ellipsoid
- Relevant Equations
- All below
fig one:
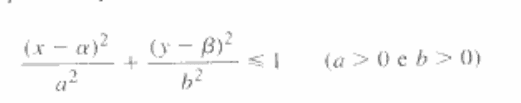
I just want to know if i am right in attack this problem by this integral:
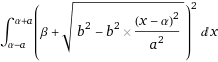 *pi
*pi
Anyway, i saw this solution:
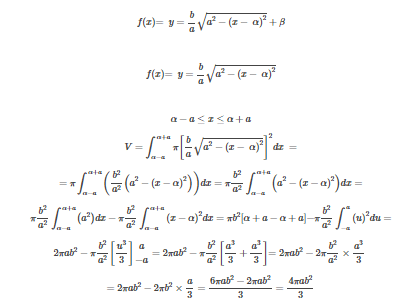
In which it cut beta, don't know why.
So i don't know.
I just want to know if i am right in attack this problem by this integral:
Anyway, i saw this solution:
In which it cut beta, don't know why.
So i don't know.