zwierz
- 334
- 62
From Painleve we know that Coulomb's law of friction being applied to rigid bodies systems may produce contradictions. Painleve constructed several examples of such contradictions, so called Painleve's paradoxes, see [Painleve P. Leçons sur le frottement. P.: Hermann, 1895]. Those examples are somewhat complicated and contain big formulas.
I would like to propose a completely trivial paradox of Coulomb's friction.
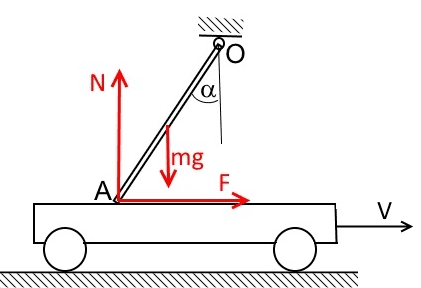
A cart moves from left to right on a horizontal road. Over the cart there is a pendulum with a fixed hing ##O## and a homogeneous rod ##OA## of mass ##m##. Rod's end ##A## rests on the cart such that the angle between the rod and the vertical is equal ##\alpha##.
Let ##N## be a normal reaction force that acts on the rod from the cart and ##F=\gamma N## be a force of friction applied to the rod; ##\gamma## is a coefficient of friction.
Applying the law of torques about the point ##O## we get
$$N=\frac{mg\sin\alpha}{2(\sin\alpha-\gamma\cos\alpha)}.$$ Thus if ##\tan\alpha<\gamma## then ##N<0## and the cart attracts the rod. That is impossible.
I would like to propose a completely trivial paradox of Coulomb's friction.
A cart moves from left to right on a horizontal road. Over the cart there is a pendulum with a fixed hing ##O## and a homogeneous rod ##OA## of mass ##m##. Rod's end ##A## rests on the cart such that the angle between the rod and the vertical is equal ##\alpha##.
Let ##N## be a normal reaction force that acts on the rod from the cart and ##F=\gamma N## be a force of friction applied to the rod; ##\gamma## is a coefficient of friction.
Applying the law of torques about the point ##O## we get
$$N=\frac{mg\sin\alpha}{2(\sin\alpha-\gamma\cos\alpha)}.$$ Thus if ##\tan\alpha<\gamma## then ##N<0## and the cart attracts the rod. That is impossible.