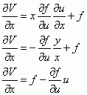Partial derivatives, change of variable

[iAlexN]

Given V=xf(u) and u = \frac{y}{x} How do you show that:

x^2 \frac{\partial^2V}{\partial x^2} + 2xy\frac{\partial^2V}{\partial x\partial y} + y^2 \frac{\partial^2V}{\partial y^2}= 0

My main problem is that I am not sure how to express V in terms of a total differential, because it is a function of x and f(u). So it depends on a variable and a function, and doesn't x also depend on u and y?

dV = \frac{\partial V}{\partial x} * dx + \frac{\partial V}{\partial f(u)} * f(u)

This total differential doesn't really help much, there must be some other way of writing it down and simplifying it?

So how should you go about solving this?

 

[sudhirking]

One way to go about the problem is to just compute the individual partial derivatives and exhibit their sum as zero. While this is brute force, when in doubt and when no simple principles seem to afford opportunity, the best you can do is just the obvious.

After taking the derivatives it does turn out that the equation is held. Carefully, exercise product rule and I recommend sticking to the variable u to the best of your ability.

 

[iAlexN]

One way to go about the problem is to just compute the individual partial derivatives and exhibit their sum as zero. While this is brute force, when in doubt and when no simple principles seem to afford opportunity, the best you can do is just the obvious.

After taking the derivatives it does turn out that the equation is held. Carefully, exercise product rule and I recommend sticking to the variable u to the best of your ability.

If I want to take the derivative of V it would look like this:

\frac{\partial V}{\partial x} = \frac{\partial}{\partial x}(xf(u))

But how would you try and evaluate that, because f(u) is some function that depends on x, u=y/x, so you wouldn't get any values out from it? Taking the derivative again, to get the second derivative, it feels like it would just continue to grow bigger with partial derivatives.

I'm clearly missing something?

 

[sudhirking]

If I want to take the derivative of V it would look like this:

\frac{\partial V}{\partial x} = \frac{\partial}{\partial x}(xf(u))

But how would you try and evaluate that, because f(u) is some function that depends on x, u=y/x,

The difficulty in the differentiation as you noted is there because of our ignorance on f(u)! But this problem is really no problem at all. For suppose, to bring light on the thing being missed, f(u) is something as simple as sin(u). Carry out derivatives if f(u) is beknown to the audience. Certainly that task will acquire no hardships other than the tedious chore of algebra.

When exercising an x partial over the sin(u) it will by virtue of chain rule, be the partial of sin(u) with respect to "u" multiplied by the partial of "u" with respect to variable x (e.g. up to a negative factor something that falls to an inverse square of x and grows conjunctly with y).

The partial of sin(u) with respect to "u" is no mystery (just the cosine). If f(u) is explicitly mentioned than the calculation is trivial. But it is not! So what do we do? The best thing we can do is leave it as a variable.

To summarize, the partial of f(u) with respect to x is the partial of f(u) with respect to "u" multiplied by the partial of "u" with x. We are forced to leave partials of f with "u" just as it is because of our own lack of specification on f, but that is ok!

Think of implicit differentiation. Suppose I had asked you what is the derivative with respect to x of the square of y. Without knowing y your answer would be

d/dx (y^2)= 2ydy/dx

Hopefully this gives you a clue on how to proceed. Note that I am trying my best not to tip over the cup of milk so to say and completely trivialize the experience by giving you the answer. I am in a sense slowly pressing you in the direction of progress.

With the above in mind though I will do the first step and provide of the derivative you had asked:

(Note I had used product rule and chain rule on any partial of f with x)

PS: I will regularly be refreshing this page so my response is not so delayed and we can have a socratic discussion of solving this problem

 

[Chestermiller]

dV=fdx+xdf
df=\frac{df}{du}du
du=\frac{xdy-ydx}{x^2}
df=\frac{df}{du}\frac{xdy-ydx}{x^2}
xdf=\frac{df}{du}(dy-udx)

 

[iAlexN]

The difficulty in the differentiation as you noted is there because of our ignorance on f(u)! But this problem is really no problem at all. For suppose, to bring light on the thing being missed, f(u) is something as simple as sin(u). Carry out derivatives if f(u) is beknown to the audience. Certainly that task will acquire no hardships other than the tedious chore of algebra.

When exercising an x partial over the sin(u) it will by virtue of chain rule, be the partial of sin(u) with respect to "u" multiplied by the partial of "u" with respect to variable x (e.g. up to a negative factor something that falls to an inverse square of x and grows conjunctly with y).

The partial of sin(u) with respect to "u" is no mystery (just the cosine). If f(u) is explicitly mentioned than the calculation is trivial. But it is not! So what do we do? The best thing we can do is leave it as a variable.

To summarize, the partial of f(u) with respect to x is the partial of f(u) with respect to "u" multiplied by the partial of "u" with x. We are forced to leave partials of f with "u" just as it is because of our own lack of specification on f, but that is ok!

Think of implicit differentiation. Suppose I had asked you what is the derivative with respect to x of the square of y. Without knowing y your answer would be

d/dx (y^2)= 2ydy/dx

Hopefully this gives you a clue on how to proceed. Note that I am trying my best not to tip over the cup of milk so to say and completely trivialize the experience by giving you the answer. I am in a sense slowly pressing you in the direction of progress.

With the above in mind though I will do the first step and provide of the derivative you had asked:

(Note I had used product rule and chain rule on any partial of f with x)

PS: I will regularly be refreshing this page so my response is not so delayed and we can have a socratic discussion of solving this problem

Thanks.

Here's my attempt at taking all the partial derivatives, it doesn't quite cancel in the end though.

\frac{\partial V}{\partial x} = f(u) - \frac{\partial f(u)}{\partial u} \frac{y}{x} = f(u) - \frac{\partial f(u)}{\partial u} u (The same as you got)

\frac{\partial V}{\partial y} = x \frac{\partial f(u)}{\partial y} = x \frac{\partial f(u)}{\partial u} \frac{\partial u}{\partial y}= x \frac{\partial f(u)}{\partial u} x = x^2 \frac{\partial f(u)}{\partial u}

\frac{\partial^2 V}{\partial^2 y} = x^2 \frac{\partial^2 f(u)}{\partial y \partial u}

 \frac{\partial^2 V}{\partial x \partial y} = 2x \frac{\partial f(u)}{\partial u} + x^2 \frac{\partial^2 f(u)}{\partial x \partial u}

One more.

\frac{\partial^2 V}{\partial^2 x} = \frac{\partial}{\partial x} f(u) - \frac{\partial}{\partial x}(\frac{\partial f(u)}{\partial u} \frac{y}{x})= \frac{\partial f(u)}{\partial u} \frac{\partial u}{\partial x} - [\frac{\partial f(u)}{\partial x \partial u} \frac{y}{x} - \frac{\partial f(u)}{\partial u} \frac{y}{x^2}] = -\frac{\partial f(u)}{\partial u}\frac{y}{x^2} - \frac{\partial f(u)}{\partial x \partial u} \frac{y}{x} + \frac{\partial f(u)}{\partial u} \frac{y}{x^2}

\frac{\partial^2 V}{\partial^2 x}= - \frac{\partial f(u)}{\partial x \partial u} \frac{y}{x}

But when I try and plug this into the equation the terms don't cancel out, so there must be some mistakes in my working?

 

[Chestermiller]

You made an algebraic error in evaluating ∂V/∂y.

Chet