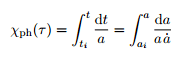SUMMARY
The integral transformation discussed is a standard application of the change of variables technique in calculus. Specifically, the equation presented is ∫ f(a(t)) dt = ∫ f(a) (dt/da) da, which illustrates how to rewrite an integral by substituting a new variable. This method is essential for simplifying integrals and is widely used in various fields, including physics and engineering. The reference provided leads to a lecture on cosmology that further elaborates on this concept.
PREREQUISITES
- Understanding of integral calculus
- Familiarity with change of variables technique
- Basic knowledge of functions and derivatives
- Exposure to applications in physics or engineering contexts
NEXT STEPS
- Study the change of variables in integrals in more depth
- Explore applications of integrals in physics, particularly in cosmology
- Learn about Jacobians and their role in multiple integrals
- Investigate advanced integral techniques such as contour integration
USEFUL FOR
Students and professionals in mathematics, physics, and engineering who are looking to deepen their understanding of integral calculus and its applications in real-world scenarios.