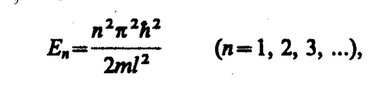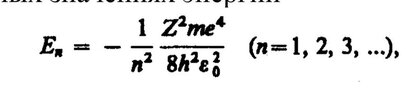Malvina
- 10
- 2
- TL;DR
- What are energies responsible for?
Hello. Help me understand the energies. The energy of a particle in a potential well, formula 1. An electron in the field of a nucleus, as an example of a particle in a potential well, and it turns out according to this formula that the further from the nucleus, the more energy is needed. And more for what?
And according to formula 2, it turns out that the further the electron is from the nucleus, the less energy it needs to break away from the nucleus.
What is the energy from the first formula "responsible" for (directly proportional to n) and what is the energy from the second formula "responsible" for (inversely proportional to n)
And according to formula 2, it turns out that the further the electron is from the nucleus, the less energy it needs to break away from the nucleus.
What is the energy from the first formula "responsible" for (directly proportional to n) and what is the energy from the second formula "responsible" for (inversely proportional to n)