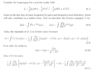SUMMARY
The discussion focuses on the path integral approach to deriving the Klein-Gordon (KG) propagator, specifically addressing issues related to the integration over momentum space and the Dirac delta function. The user seeks clarification on how to correctly derive the delta function in equation (6.9) and emphasizes the importance of using the Feynman propagator, represented as $$\Delta(p)=\frac{1}{p^2-m^2+\mathrm{i} 0^+}$$. Key points include the necessity of using separate momentum variables for the field terms and the inclusion of the factor of ##i## in the source term integration.
PREREQUISITES
- Understanding of path integral formulation in quantum field theory
- Familiarity with Klein-Gordon propagator and its significance
- Knowledge of Fourier transforms in the context of quantum mechanics
- Basic concepts of operator perturbation theory
NEXT STEPS
- Study the derivation of the Feynman propagator in quantum field theory
- Explore the implications of the ##\mathrm{i} 0^+## term in propagator calculations
- Review the integration techniques used in path integrals, particularly in momentum space
- Examine Section 1.10 of the provided lecture notes for non-relativistic path integral derivations
USEFUL FOR
Students and researchers in theoretical physics, particularly those focusing on quantum field theory, path integrals, and propagator calculations.