You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is Quantum field theory: Definition and 567 Discussions
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles.
QFT treats particles as excited states (also called quanta) of their underlying quantum fields, which are more fundamental than the particles. Interactions between particles are described by interaction terms in the Lagrangian involving their corresponding quantum fields. Each interaction can be visually represented by Feynman diagrams according to perturbation theory in quantum mechanics.
View More On Wikipedia.org
QFT treats particles as excited states (also called quanta) of their underlying quantum fields, which are more fundamental than the particles. Interactions between particles are described by interaction terms in the Lagrangian involving their corresponding quantum fields. Each interaction can be visually represented by Feynman diagrams according to perturbation theory in quantum mechanics.
View More On Wikipedia.org
-
M
High Energy Possible typo in Peskin & Schroeder's QFT Textbook (p. 666)?
Hi everyone! I'm going through Peskin & Schroeder's Chapter 19 (Perturbation Theory Anomalies) and it seems to be that equation 19.74 in page 666 has a minus sign missing on the RHS. Namely, I think the correct equation should read \begin{align} (i\not\!\! D)^2 = -D^2 -...- murillo137
- Thread
- Replies: 5
- Forum: Science and Math Textbooks
-
B
Equations of motion for Lagrangian of scalar QED
Well, I started with the first equation of motion for the scalar field, but I'm really not sure if I'm doing it the right way. \begin{equation} \begin{split} \frac{\partial \mathcal{L}}{\partial \varphi} &= \frac{\partial}{\partial \varphi} [(\partial_\mu \varphi^* -...- BobaJ
- Thread
- Replies: 0
- Forum: Advanced Physics Homework Help
-
O
I Vacuum decay likelihood and consequences
what is the likelihood of a vacuum decay happening, like is it something that is really considered and taken seriously by scientists or is it just wild speculation that is not really taken seriously but makes for good headlines? Also if vacuum decay does happen what exactly would be the...- OCD
- Thread
- Replies: 0
- Forum: Quantum Physics
-
P
High Energy What is the level of Aitchison & Hey's QFT books?
I'm talking about their two volume set titled "Gauge Theories in Particle Physics". Amazon links: Volume 1 Volume 2 From looking at the books, it seems that the level is higher compared to Griffiths or Thomson. But, how does it compare to textbooks like Peskin & Schroeder or Schwartz...- particlesandpoems
- Thread
- Replies: 1
- Forum: Science and Math Textbooks
-
K
I Is conservation of energy a local law in Quantum field theory?
From Wikipedia, I know that it is the case in GR that conservation of energy and other conservation laws are relegated to being local only I thought this wasn't the case in quantum field theory.- KleinMoretti
- Thread
- Replies: 18
- Forum: Quantum Physics
-
H
A Derivation of QM limit of QFT in "QFT and the SM" by Schwartz
In this derivation, a basis of one-particle states ##\langle x|=\langle \vec x,t|## is expressed with the field operator, $$\langle x|=\langle 0| \phi (\vec x, t)$$ "Then, a Schrodinger picture wavefunction is $$\psi (x)=\langle x| \psi \rangle$$ which satisfies $$i \partial _t \psi (x) = i...- Hill
- Thread
- Replies: 2
- Forum: Quantum Physics
-
H
I Are All Photons Truly Virtual?
My understanding is (was) that "virtual particles" is a computational concept used in perturbation calculations in QFT e.g. in Feynman diagrams. This understanding is in conflict with the following note in Quantum Field Theory for the Gifted Amateur by Tom Lancaster and Stephen J. Blundell: and...- Hill
- Thread
- Replies: 6
- Forum: Quantum Physics
-
D
I Exploring Measurements in Quantum Field Theory: From Light Cones to Bell Tests
Hello, I'm interested in how measurement, entanglement, bell test etc are handled in QFT. It seems most QFT texts are being quite light on details on the subject. There would be is a preparation step as the start followed by some interaction and a measurement at the end. Interaction is usually...- Delta Kilo
- Thread
- Replies: 57
- Forum: Quantum Interpretations and Foundations
-
P
Studying Should I study relativistic QFT to get non-relativistic QFT?
First time in PF, I am sorry if I did not choose the right category. I have been doing theory in condensed matter (mostly numerics) as a PhD but I never got to learn proper quantum field theory (QFT). Aside from a few introductory courses at university, I never learned what is a many-body...- pines-demon
- Thread
- Replies: 10
- Forum: STEM Academic Advising
-
B
A Dimensional Regularization
Hi guys! I was wondering if there is any difference choosing between d = 4 -e or d = 4 - 2e. If so, what are the impacts ?- Break1
- Thread
-
- Tags
- Quantum field theory
- Replies: 4
- Forum: High Energy, Nuclear, Particle Physics
-

Lorentz boost generator commutator
Using above formula, I could calculate the given commutator. $$ [\epsilon^{\mu\nu\rho\sigma} M_{\mu \nu}M_{\rho\sigma},M_{\alpha\beta}]=i\epsilon^{\mu\nu\rho\sigma}(M_{\mu \nu}[M_{\rho\sigma},M_{\alpha\beta}]+[M_{\rho\sigma},M_{\alpha\beta}]M_{\mu \nu}) $$ (because...- han
- Thread
- Replies: 2
- Forum: Advanced Physics Homework Help
-
M
A Uncovering the Combinatorial Origins of Yang-Mills Theory?
For many years now, the theorist Nima Arkani-Hamed has lent his prestige and energy to a research program that aims to transform our understanding of quantum field theory, by using symmetries in the sums of Feynman diagrams to uncover perspectives on the theory not based in ordinary space-time...- mitchell porter
- Thread
- Replies: 0
- Forum: Beyond the Standard Models
-

A The Quantum State as a Function of The Quantum Field
In answering another question, I came across a nice paper by Weinberg: https://www.arxiv-vanity.com/papers/hep-th/9702027/ One thing that struck me was the following comment: 'In its mature form, the idea of quantum field theory is that quantum fields are the basic ingredients of the...- bhobba
- Thread
- Replies: 13
- Forum: Quantum Interpretations and Foundations
-

A The relation between ferromagnets, Phi4 and non-linear sigma model
I'm struggling to understand the relation between phi4 theory,non-linear sigma model and ferromagnets. I've read this in a paper(Phys.Rev.B14(1976)3110):'It is possible to describe the long-distance behavior of the Heisenberg ferromagnets in two different ways:the phi4 theory which corresponds...- Aethermimicus
- Thread
- Replies: 0
- Forum: Atomic and Condensed Matter
-
T
A Understanding Ghost Fields in QED: Eliminating Unphysical Degrees of Freedom"
I have a question about following statement about ghost fields in found here : It states that introducing some ghost field provides one way to remove the two unphysical degrees of freedom of four component vector potential ##A_{\mu}## usually used to describe the photon field, since physically...- The Tortoise-Man
- Thread
- Replies: 9
- Forum: Quantum Physics
-
W
Other What are areas of research that pertain to Grand Unified Theory?
I am planning on pursing a Phd in Theoretical physics or Mathematical Physics in the next several years. My main motivation is doing research when it comes to grand unified theory. What areas of research (within that umbrella, in a theoretical sense) should I start looking into that are at the...- wyattbohr
- Thread
- Replies: 1
- Forum: STEM Academic Advising
-
C
Noether current in quantum field theory
Hi Have been trying to solve the below question for a while, wondered if anyone could help. Considering the action $$S=\int -\frac{1}{2}\sum^2_{n,m=1} (\partial^{\mu}\phi_{nm}\partial_{\mu}\phi_{mn}+m^2 \phi_{nm} \phi_{mn})dx$$ under the transformation $$\phi'=e^{\alpha}\phi e^{-\alpha}$$...- CSpring432
- Thread
-
- Tags
- Quantum field theory
- Replies: 1
- Forum: Advanced Physics Homework Help
-
P
Schwartz's Quantum field theory, (14.100) Fermionic path integral
I am reading the Schwartz's Quantum field theory, p.269~p.272 ( 14.6 Fermionic path integral ) and some question arises. In section 14.6, Fermionic path integral, p.272, (14.100), he states that $$ \int d\bar{\theta}_1d\theta_1 \cdots d\bar{\theta}_n d\theta_n e^{-\bar{\theta}_i A_{ij}...- Plantation
- Thread
-
- Tags
- Quantum field theory
- Replies: 2
- Forum: Advanced Physics Homework Help
-
T
A How can I calculate the square of the Pauli-Lubanski pseudovector?
Hello there, recently I've been trying to demonstrate that, $$\textbf{W}^2 = -m^2\textbf{S}^2$$ in a rest frame, with ##W_{\mu}## defined as $$W_{\mu} = \dfrac{1}{2}\varepsilon_{\mu\alpha\beta\gamma}M^{\alpha\beta}p^{\gamma}$$ such that ##M^{\mu\nu}## is an operator of the form $$...- tannhaus
- Thread
- Replies: 1
- Forum: Special and General Relativity
-
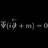
A Solving renormalization group equation in QFT
I'm learning about the RG equation and Callan-Symanzik equation. In ref.1 they claim to solve the RG equation via the method of characteristics for PDE. Here's a picture of the relevant part: First, the part I don't understand - the one underlined in red. What does "compatible" mean here...- qft-El
- Thread
- Replies: 5
- Forum: Quantum Physics
-
S
A Renormalized vertex functions in terms of bare ones
Let ##\Gamma[\varphi] = \Gamma_0[\sqrt{Z}\varphi ] = \Gamma_0[\varphi_0]## be the generating functional for proper vertex functions for a massless ##\phi##-##4## theory. The ##0## subscripts refer to bare quantities, while the quantities without are renormalized. Then $$\tilde{\Gamma}^{(n)}(p_i...- Siupa
- Thread
- Replies: 0
- Forum: Quantum Physics
-
P
Differentiation of functional integral (Blundell Quantum field theory)
I am reading the Lancaster & Blundell, Quantum field theory for gifted amateur, p.225 and stuck at understanding some derivations. We will calculate a generating functional for the free scalar field. The free Lagrangian is given by $$ \mathcal{L}_0 = \frac{1}{2}(\partial _\mu \phi)^2 -...- Plantation
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
T
A Quantization of real Klein-Gordon field (sign issues)
I have a pretty naive question about quantization of real Klein-Gordon (so scalar) field ##\hat{\phi}(x,t)##. The most conventional form (see eg in this one ; but there are myriad scripts) is given by ##\hat{\phi}(x,t)= \int d^3p \dfrac{1}{(2\pi)^3} N_p (a_p \cdot e^{i(\omega_pt - p \cdot...- The Tortoise-Man
- Thread
- Replies: 24
- Forum: Quantum Physics
-
Y
A Lagrangian in the Path Integral
Using free scalar field for simplicity. Hi all, I have a question which is pretty simple, we have the path integral in QFT in the presence of a source term: $$ Z[J] = \int \mathcal{D}\phi \, e^{i \int d^4x \left( \frac{1}{2} \phi(x) A \phi(x) + J(x) \phi(x) \right)} $$ So far so good. Now...- YeaNah
- Thread
- Replies: 13
- Forum: Quantum Physics
-
P
This integration appeared in the reconstruction of cross section
I am reading the Horatiu Nastase's Introduction to quantum field theory (https://professores.ift.unesp.br/ricardo.matheus/files/courses/2014tqc1/QFT1notes.pdf ) ( Attached file ) or Peskin, Schroeder's quantum field theory book, p.105, (4.77). Through p.176 ~ p. 177 in the Nastase's Note, he...- Plantation
- Thread
- Replies: 15
- Forum: Advanced Physics Homework Help
-
S
I All possible QFTs from geometry?
Physicist Nima Arkani-Hamed has taken an approach to understand fundamental physics based on geometry (specifically, positive geometry). This started with his work with Jaroslav Trnka in the amplituhedron [1] and later it was generalised to the associahedron [2],the EFT-hedron [3]... I was...- Suekdccia
- Thread
- Replies: 3
- Forum: Beyond the Standard Models
-
O
Deriving Maxwell's equations from the Lagrangian
This isn't a homework problem (it's an example from David Tong's QFT notes where I didn't understand the steps he took), but I am confused as to how exactly to take the partial derivative of the Lagrangian with respect to ##\partial(\partial_\mu \mathcal{A}_\nu)##. (Note the answer is...- offscene
- Thread
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
T
A What exactly does 'Locality' in Gauge Theory mean?
What means exactly the principle of 'locality' in context of gauge theory? Motivation: David Tong wrote in his notes on Gauge Theory (p 115): "their paper (the 'original' paper by Yang & Mills introducing their theory) suggests that global symmetries of quantum f ield theory– specifically SU(2)...- The Tortoise-Man
- Thread
- Replies: 5
- Forum: Quantum Physics
-

A Asymptotic states in the Heisenberg and Schrödinger pictures
In scattering theory, the quantity of interest is the amplitude for the system—initially prepared as a collection of (approximate) momentum eigenstates—to evolve into some other collection of momentum eigenstates. For example, for ##m\to n## scattering, the amplitude we're interested in is...- UnreliableObserver
- Thread
- Replies: 8
- Forum: Quantum Physics
-

I Spontaneous Symmetry Breaking and quantum mechanics
Confronted with my inability to grasp Witten's Susy QM examples of supersymmetry breaking, I concluded that the problem was that I was not understanding spontaneous symmetry breaking in simpler contexts. It seems that SSB is not possible in QM because of tunneling between the different states...- arivero
- Thread
- Replies: 15
- Forum: Quantum Physics
-
P
I Confusion about Scattering in Quantum Electrodynamics
When it comes to scattering in QED it seems only scattering cross sections and decay rates are calculated. Why is that does anyone calculate the actual evolution of the field states or operators themselves like how the particles and fields evolve throughout a scattering process not just...- physwiz222
- Thread
- Replies: 134
- Forum: Quantum Physics
-
D
Question related to completeness relation for photons
Hi Would you explain to me what is the q^ and how they are related to completeness.How can i solve this exercise?It is from "Quarks and leptons An Introductory course in Modern Particle Physics" of Halzen and Alan D.Martin.Also, can you point me to a useful bibliography?- Dhmht_Kr
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Deriving the commutation relations of the Lie algebra of Lorentz group
This is the defining generator of the Lorentz group which is then divided into subgroups for rotations and boosts And I then want to find the commutation relation [J_m, J_n] (and [J_m, K_n] ). I'm following this derivation, but am having a hard time to understand all the steps: especially...- bella987
- Thread
- Replies: 3
- Forum: Advanced Physics Homework Help
-
R
Expressing Feynman Green's function as a 4-momentum integral
I am a bit confused on how we can just say that (z',p) form a 4-vector. In my head, four vectors are sacred objects that are Lorentz covariant, but now we introduced some new variable and say it forms a 4-vector with momentum. I understand that these are just integration variables but I still do...- realanswers
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-

I Finding ##\partial^\mu\phi## for a squeezed state in QFT
I'm trying to apply an operator to a massless and minimally coupled squeezed state. I have defined my state as $$\phi=\sum_k\left(a_kf_k+a^\dagger_kf^*_k\right)$$, where the ak operators are ladder operators and fk is the mode function $$f_k=\frac{1}{\sqrt{2L^3\omega}}e^{ik_\mu x^\mu}$$...- Sciencemaster
- Thread
- Replies: 2
- Forum: Quantum Physics
-
A
A Schrodinger equation in quantum field theory
What is the Schrodinger equation in QFT? is it the nonrelativistic approximation of a Klein-Gordon scalar field? or Is there more? I have read that the Schrodinger equation describes a QFT in 0 dimensions. I accept every answer- accdd
- Thread
- Replies: 8
- Forum: Quantum Physics
-
C
A Multiparticle Relativistic Quantum Mechanics in an external potential
It is often argued that Dirac Equation is not valid as relativistic quantum mechanics requires the creation of antiparticles. But, there are also some arguments that suggest otherwise. For example, I saw Arnold Neumaier's website on this that there are multiparticle relativistic quantum...- curious_mind
- Thread
- Replies: 22
- Forum: Quantum Physics
-
M
Non quadratic potentials and quantization in QFT (home exercise)
I noticed that ##V(\phi)## has nonzero minima, therefore I found the stationary points as ##{{\partial{V}}\over{\partial\phi}}=0##, and found the solutions: $$\phi^0_{1,2}=-{{m}\over{\sqrt{\lambda}}}\quad \phi^0_3={{2m}\over{\sqrt{\lambda}}}$$ of these, only ##\phi^0_3## is a stable minimum... -
V
I Uncertainty Principle in QFT & Early Universe Conditions
I have a question related to the uncertainty principle in QFT and if it is related to the early universe conditions. Do we still have four-vector momentum and position uncertainty relation in relativistic quantum theory? I have been following the argument related to the early universe and the... -
D
I Equation which is related with the Lorentz invariant quantities
Hi every one.How can i prove the below equation? And then that it's Lorentz invariant quantitude ? Thanks for your help- Dhmht_Kr
- Thread
- Replies: 1
- Forum: High Energy, Nuclear, Particle Physics
-
L
B Quantum field theory and wave particle duality
I recently watched this lecture "Quantum Fields: The Real Building Blocks of the Universe" by David Tong where the professor provides a succinct explanation of QFT in about 6 minutes around the midway mark. The main point being that there are fields for particles and fields for forces and the...- LifelongLearner125
- Thread
- Replies: 2
- Forum: Quantum Physics
-
R
Addressing Misconceptions in Popular Science: A Call for Clear Communication
I am not a Physicist. I am a retired Social Worker and Public Health Administrator who has taken an interest in Cosmology and Quantum Mechanics/Quantum Field Theory. I am reading as much popular literature in the field as I can as well as watching the excellent presentations on YouTube. I try...- RussZ
- Thread
- Replies: 14
- Forum: New Member Introductions
-
A Ensembles in quantum field theory
Then please explain how the transition in conceptual language from a single quantum field (extending all over spacetime, or at least over the lab during a day) to an ensemble of particles can be justified from the QFT formalism.- A. Neumaier
- Thread
- Replies: 91
- Forum: Quantum Interpretations and Foundations
-

High Energy Literature for introduction to O(N) vector model
TL;DR Summary: Looking for literature on O(N) vector model Hello, We have been going over the O(N) vector model in my QFT class but the notes are not very detailed and we are not using a textbook. Does anyone know of a good QFT book which goes over this material? I have a copy of Shrednicki...- josephsanders
- Thread
- Replies: 9
- Forum: Science and Math Textbooks
-

I Unruh, Haag et al.: No Room for Particles in Quantum Field Theory?
In a paper by Bain (2011), particles are left with little ontological value because of the Reeh-Schlieder theorem, the Unruh effect and Haag's theorem. The author claims (and here I am copying his conclusion): First, the existence of local number operators requires the absolute temporal metric...- lindberg
- Thread
- Replies: 12
- Forum: Quantum Physics
-

I Has the Unruh Effect ever been observed?
A recent paper (June 2021) claims to have observed the Unruh effect: https://arxiv.org/abs/1903.00043 A more recent article (with links to the papers inside it) talks about a possible way to detect it (Barbara Soda et al., April 2022), while there are still skeptics (Anatoly Svidzinsky). Here is...- lindberg
- Thread
- Replies: 13
- Forum: Quantum Physics
-

I Haag's Theorem: Explain Free Field Nature
What is the main reason for a free field staying free according to Haag's theorem?- lindberg
- Thread
- Replies: 4
- Forum: Quantum Physics
-
R
I Interpreting ##A^{\mu}(x)|0\rangle## and ##\psi (x) |0\rangle##
I can understand how ##\phi (x)|0\rangle## represents the wavefunction of a single boson localised near ##x##.I don't understand how the same logic appies to ##A^{\mu}(x)|0\rangle## and ##\psi |0\rangle##. Both of these operators return a four component wavefunction when operated on the vaccuum...- Ryder Rude
- Thread
- Replies: 5
- Forum: Quantum Physics
-

A How to take non-relativistic limit of the following Lagrangian
In https://arxiv.org/pdf/1709.07852.pdf, it is claimed in equation (1) and (2) that when we take non-relativistic limit, the following Lagrangian (the interaction part) $$L=g \partial_{\mu} a \bar{\psi} \gamma^{\mu}\gamma^5\psi$$ will yield the following Hamiltonian $$H=-g\vec{\nabla} a \cdot...- Tan Tixuan
- Thread
- Replies: 1
- Forum: High Energy, Nuclear, Particle Physics
-
A Exploring the Limits of Quantum Mechanics: David Wallace's Manuscript (2022)
David Wallace, The sky is blue, and other reasons quantum mechanics is not underdetermined by evidence, Manuscript (2022). arXiv:2205.00568. From the Abstract: ''I argue that there as yet no empirically successful generalization of'' [Bohmian Mechanics and dynamical-collapse theories like the...- A. Neumaier
- Thread
- Replies: 22
- Forum: Quantum Interpretations and Foundations