SUMMARY
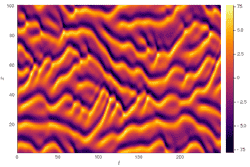
The discussion highlights the Kuramoto–Sivashinsky equation, a fourth-order partial differential equation (PDE) utilized in modeling flame dynamics. It also references the Korteweg–de Vries (KdV) soliton equation, significant in nonlinear physics, and the Euler-Bernoulli beam theory, which describes one-dimensional transverse waves in slender beams. These examples illustrate the practical applications of high-order PDEs in various scientific fields.
PREREQUISITES
- Understanding of partial differential equations (PDEs)
- Familiarity with the Kuramoto–Sivashinsky equation
- Knowledge of the Korteweg–de Vries (KdV) soliton equation
- Basic principles of the Euler-Bernoulli beam theory
NEXT STEPS
- Research the applications of the Kuramoto–Sivashinsky equation in combustion modeling
- Explore the Korteweg–de Vries equation and its role in soliton theory
- Study the Euler-Bernoulli beam theory in the context of structural engineering
- Investigate other high-order PDEs and their applications in physics and engineering
USEFUL FOR
Researchers, physicists, and engineers interested in advanced applications of partial differential equations in real-world scenarios, particularly in combustion, fluid dynamics, and structural analysis.
https://en.wikipedia.org/wiki/Kuramoto–Sivashinsky_equation