S. Moger
- 52
- 2
In many games a pair of standard six sided dice is used. I denote this 2d6.
In this particular game, if a die is rolled the result is registered. If it returned a 6, it is re-rolled while a 5 is recorded. So it's basically a 2d5+1 open ended roll, which in theory could end up with very large numbers.
Anyway, the expected value of one such roll is 4, which if written out as a series, can be calculated like this \sum_{n=1}^{\infty} \frac{5\cdot3+5}{6^n} = 20/5 = 4. It can be generalized to show that introducing the open endedness (i.e. dn+1) adds 1/2 to the average of dn.
For two dice in 2d5+1 arrangement the average is 8 compared to the 7 of 2d6.
That is all great, but now I want a function that returns the probability of 2d5+1 beating a roll of 2d5+1 plus an arbitrary integer c, i.e.
f(c) = P([\mathit{2d5+1}]_1 > [\mathit{2d5+1}]_2 + c)
To get an impression of the problem I tried drawing some approximate graphs by enumerating the sums of the "display values" of a 2d5+1 dice roll and pairing them with the probabilities of them containing at least one 6 and thus computing the average "return values" using the known average computed before. From 2-6 the display values equal the actual values. From 7 to 10 one six can be present. At 11, one six is present, and at 12, both are. With this simplified approach 18 is the highest return value though.
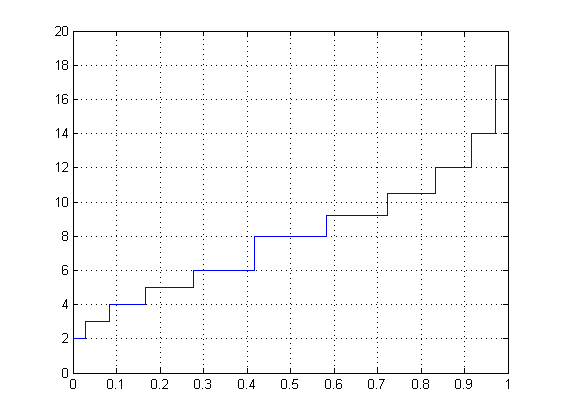
And a sketch of the PDF:
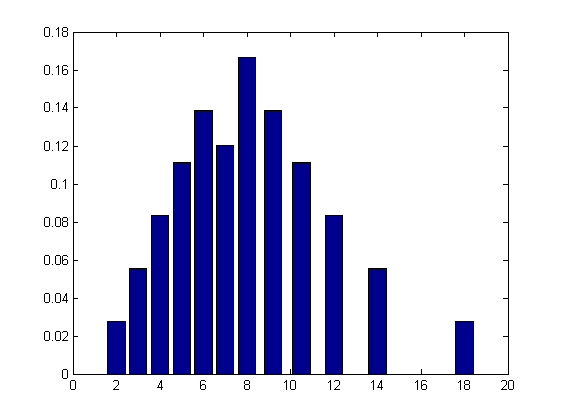
This PDF (roughly) shows the return values of 2-6 and values that included a six as display value + the average of the next roll (apart from the bar for 7 which I added in manually). The real values would have to include some more data from non-six contributions. In any case, it would seem that some return values are drained in favor of increasing the span to the right. However, it would be interesting to populate the graphs above and to make them exact, incl. obtaining an expression for
f(c) = P([\mathit{2d5+1}]_1 > [\mathit{2d5+1}]_2 + c)
In this particular game, if a die is rolled the result is registered. If it returned a 6, it is re-rolled while a 5 is recorded. So it's basically a 2d5+1 open ended roll, which in theory could end up with very large numbers.
Anyway, the expected value of one such roll is 4, which if written out as a series, can be calculated like this \sum_{n=1}^{\infty} \frac{5\cdot3+5}{6^n} = 20/5 = 4. It can be generalized to show that introducing the open endedness (i.e. dn+1) adds 1/2 to the average of dn.
For two dice in 2d5+1 arrangement the average is 8 compared to the 7 of 2d6.
That is all great, but now I want a function that returns the probability of 2d5+1 beating a roll of 2d5+1 plus an arbitrary integer c, i.e.
f(c) = P([\mathit{2d5+1}]_1 > [\mathit{2d5+1}]_2 + c)
To get an impression of the problem I tried drawing some approximate graphs by enumerating the sums of the "display values" of a 2d5+1 dice roll and pairing them with the probabilities of them containing at least one 6 and thus computing the average "return values" using the known average computed before. From 2-6 the display values equal the actual values. From 7 to 10 one six can be present. At 11, one six is present, and at 12, both are. With this simplified approach 18 is the highest return value though.
And a sketch of the PDF:
This PDF (roughly) shows the return values of 2-6 and values that included a six as display value + the average of the next roll (apart from the bar for 7 which I added in manually). The real values would have to include some more data from non-six contributions. In any case, it would seem that some return values are drained in favor of increasing the span to the right. However, it would be interesting to populate the graphs above and to make them exact, incl. obtaining an expression for
f(c) = P([\mathit{2d5+1}]_1 > [\mathit{2d5+1}]_2 + c)