Perimeter relationships -- Dividing a rectangle into 4 triangles

[althea_saile]

Hello,

I am studying geometry with an app on my phone. There was a difficult problem, which had two different explanations for solving. I correctly understood one explanation. I reviewed later without memory of the problem at all. There was an obvious attempt from what was learned previously, but I discovered something more perhaps! I creatively guessed at a new explanation due to my lack of memory. I guessed the answer correctly with a different understanding of the method solution used.

Spoiler

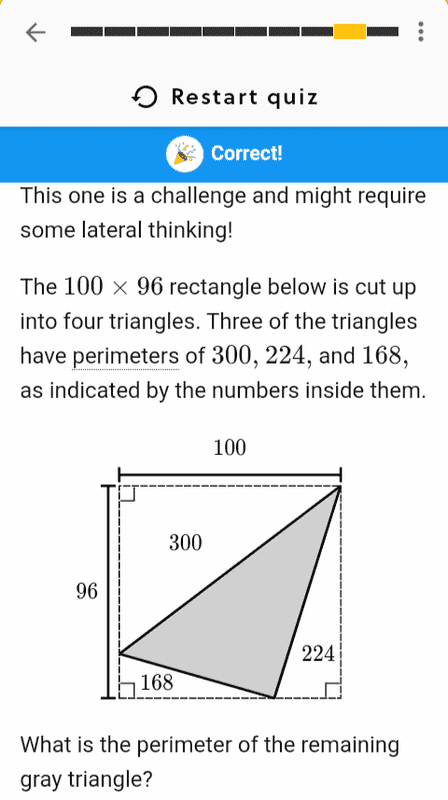The explanation #2 that I initially answered correct: "The perimeter of the gray triangle is equal to the difference between the sum of triangle periemeters and the perimeter of the square. The perimeter of the square is 2 X 96 + 2 X 100 = 392, while the sum of the triangle perimeters is 224 + 168 + 300 = 692. The perimeter of the gray triangle is 692 - 392= 300."

Memory-less review of the problem: There seems to be some kind of relation between perimeter of a shape & smaller shape perimeters inside that encompassing shape. I don't have the know-how or tools to experiment with this theory. How do I come up with the perimeter of a random shape, with included smaller perimeters inside that shape for play at this idea--like a teacher? When, where, and why does this seem to be true? I'll note down what I CAN do, without coming up with an experiment, then search the internet. I noticed that there are 4 sides to the rectangle, which is conveniently the number of smaller shapes inside of it. Does this mean that a polygon with n-sides has a perimeter relationship to the perimeters of inscribed n-polygons summated? Another thought I had was that it would have to be n-sided polygon minus one for the summation relation of the perimeter to work... Perhaps it does but it is out of my knowledge base to test this. I searched google to no avail.Hopefully my line of thought makes sense & someone here has something to say about this please! thank you.

 

[willem2]

The perimeter of a shape made of several subshapes, is equal to the sum of the perimeters of the subshapes minus the length of all the lines that you double counted, because they belong to the perimeter of two of the supshapes.

You can also call name two sides of one of the triangles, X and Y and compute all the other lengths as a function of X and Y. You'll also have sqrt (X^2 + Y^2) + x + y = 168, for example, but you can ignore that.
The perimeter of the triangle will be independent of X and Y anyway.

 

[Office_Shredder]

Yeah, I wouldn't try to memorize a theorem here or anything, since I don't think anything exists and if it does it's very specific. The way I would approach a problem like this is to write down variable names for the lengths of every line, and write down the formula I'm looking for (the sum of the the interior lines) and the information given (the sum of the three lines forming each triangle). If you add all your equations together you'll see you get that formula you are looking for.