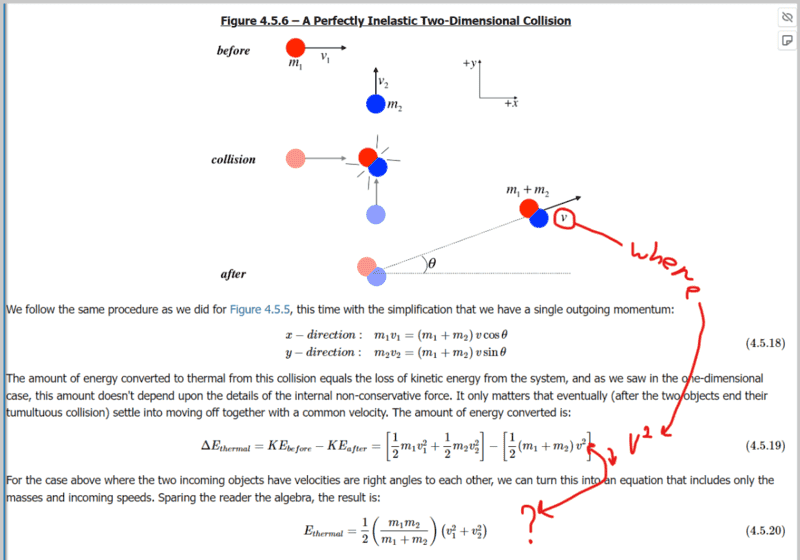
The discussion centers on the derivation of equations related to perpendicular inelastic collisions, specifically addressing the disappearance of the variable "v" in the calculations. Participants highlight the importance of solving the system of equations 4.5.18 to find "v," which is dependent on the masses (m1, m2) and initial velocities (v1, v2) of the colliding objects. The final result is expressed in equation 4.5.20 after substituting "v" into equation 4.5.19 and performing algebraic manipulations. Additionally, a general formula for energy loss in one-dimensional inelastic collisions is presented, emphasizing the role of reduced mass and relative velocity.
PREREQUISITESPhysics students, educators, and anyone studying mechanics, particularly those focused on collision theory and energy conservation principles.
There's a general result (which can be derived) for energy loss in a 1 dimensional inelastic (collide and coalesce) collision: $$\Delta E= \frac{1}{2} \mu \Delta v^2$$ where ##\mu## is the reduced mass of the colliding objects and ##\Delta v## their relative velocity: $$\mu = \frac{m_1m_2}{m_1+m_2}$$It looks like there's nothing different here except that ##\Delta v## is replaced by the vector difference of the two velocities.NODARman said: