A block falling onto a spring (SHM related question)

[Tea_Aficionado]

Homework Statement

A block of mass m = 2.0kg is dropped from a height h = 0.45m, above an uncompressed spring as shown here. The spring has an elastic constant k = 200 N/m and negligible mass. The block strikes the end of the spring and sticks to it.

a. Determine the speed of the block at the instant it hits the end of the spring
b. Determine the force in the spring when the block reaches the equilibrium position
c. Determine the distance that the spring is compressed at the equilibrium position
d. Determine the speed of the block at the equilibrium position
e. Determine the resulting amplitude of the oscillation that ensues
f. Is the speed of the block a maximum at the equilibrium position, explain
g. Determine the period of the SHM that ensues

Relevant Equations

Please see below

EDIT for clarity: I solved the question, just asking for if the explanations make sense and if the mechanical energy is considered to be conserved before and after the collision due to reasons listed below the photo.

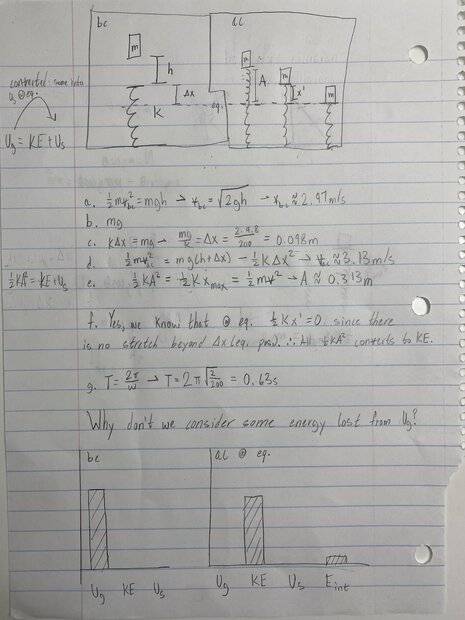
I hope this image is readable (grr, scanner is janky).

I'm guessing the answer (to the question at the bottom of the paper) is again, due to ideality and therefore conservation of mechanical energy. And as haru has pointed out earlier, it doesn't matter whether the collision was elastic or inelastic because the spring is considered to be ideal, and therefore has negligible mass and should be ignored.

(Also: do the answers' explanations make sense?)

 

[anuttarasammyak]

An usual way is to use conservation of energy, i.e.
$$\frac{1}{2}mv^2+\frac{1}{2}kx^2+mgx=const.$$
where x =0 at initial end's height of the spring.