jollage
- 61
- 0
Hi All,
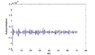
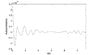
I was in a process of processing my vibration-test data. I now generated a plot of the autocorrelation function of the object acceleration. Please see the attachements (the second attachment is the close-up for small tau's).
The x-axis in the plot is the time delay tau. You can see from the second attachment that, at tau=0,the autocorrelation reaches its maximum.
My question is, as for the signal like this, in the long time delay (tau=60s, 70s), the autocorrelation still does not decay too much. What could this behavior imply? In terms of the noise frequency, what can we say?
Any comments will be welcome. Thanks in advance.
Mz
I was in a process of processing my vibration-test data. I now generated a plot of the autocorrelation function of the object acceleration. Please see the attachements (the second attachment is the close-up for small tau's).
The x-axis in the plot is the time delay tau. You can see from the second attachment that, at tau=0,the autocorrelation reaches its maximum.
My question is, as for the signal like this, in the long time delay (tau=60s, 70s), the autocorrelation still does not decay too much. What could this behavior imply? In terms of the noise frequency, what can we say?
Any comments will be welcome. Thanks in advance.
Mz
Attachments
Last edited: