- #1
ElijahRockers
Gold Member
- 270
- 10
I'm trying to design a program that can accurately detect the frequency of a real, periodic audio signal, such as several guitar notes in sequence.
I have the skeleton of the program working. It does, at times, accurately detect the frequency. However, it is very noisy, and I'm not too sure how to fix it. I believe it is an issue with how I'm finding the period of the auto-correlations.
Right now I (try to) search for the second peak of the auto correlation by ignoring the first, initial peak, then finding the next local max. (By definition, greater than the two values before and after it).
I'm not too concerned with the floor noise right now, as I don't think that's my problem.
If anyone has any suggestions on how to improve the quality/readability of the program, I would greatly appreciate it.
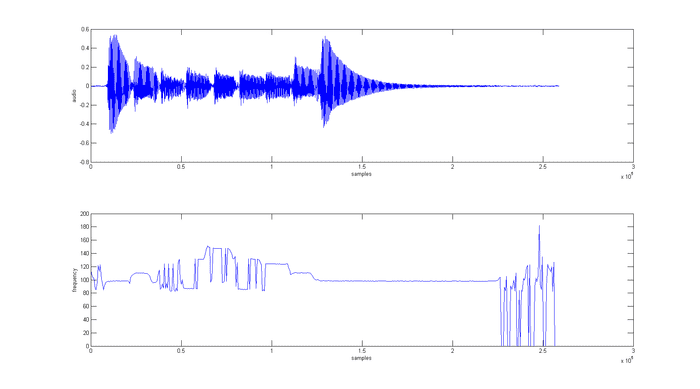
The image is a graph of me running up then back down the G Major scale on an acoustic guitar.
As you can see, it KINDA works. The first two and last three notes are correct, but the notes in between have issues.
Link to code:
https://gist.github.com/elijahrockers/1e9f1ece4fcc546d756b
I have the skeleton of the program working. It does, at times, accurately detect the frequency. However, it is very noisy, and I'm not too sure how to fix it. I believe it is an issue with how I'm finding the period of the auto-correlations.
Right now I (try to) search for the second peak of the auto correlation by ignoring the first, initial peak, then finding the next local max. (By definition, greater than the two values before and after it).
I'm not too concerned with the floor noise right now, as I don't think that's my problem.
If anyone has any suggestions on how to improve the quality/readability of the program, I would greatly appreciate it.
The image is a graph of me running up then back down the G Major scale on an acoustic guitar.
As you can see, it KINDA works. The first two and last three notes are correct, but the notes in between have issues.
Link to code:
https://gist.github.com/elijahrockers/1e9f1ece4fcc546d756b
Last edited: