SUMMARY
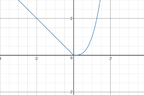
The easiest way to graph a piecewise-defined function by hand involves plotting each segment separately on the same xy-plane. For the function defined as y(x) = |x| for x ≤ 0 and y(x) = x^3 for x > 0, the upper piece is represented by the line y = -x on the interval (-∞, 0], while the lower piece is represented by the cubic function y = x^3 on the interval (0, ∞). Utilizing tools like Wolfram can enhance the graphing process, but manual plotting is straightforward and effective.
PREREQUISITES
- Understanding of piecewise-defined functions
- Familiarity with graphing linear and cubic functions
- Basic knowledge of coordinate systems
- Experience with mathematical notation and expressions
NEXT STEPS
- Learn how to graph piecewise functions using Desmos
- Explore the properties of cubic functions and their transformations
- Study the concept of continuity in piecewise functions
- Investigate the use of Wolfram Alpha for advanced graphing techniques
USEFUL FOR
Students, educators, and anyone interested in mastering the graphing of piecewise-defined functions, particularly in algebra and calculus contexts.