- #1
mcastillo356
Gold Member
- 560
- 267
- TL;DR Summary
- A quote from the maths textbook Calculus, by Robert A. Adams and Christopher Essex, and a graph I should conceptually connect, but do not.
Hi PF
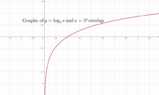
The logarithm is the inverse function to exponentiation. But, focusing on exponentiation, here comes the graph:

And, next, the quote
An exponential function is a function of the form ##f(x)=a^x##, where the base ##a## is a positive constant and the exponent ##x## is the variable.
Observe that ##a^x>0## for all ##a>0## and all real ##x## and that
If ##a>1##, then ##\lim_{x\rightarrow -\infty}{a^x=0}## and ##\lim_{x\rightarrow \infty}{a^x=\infty}##
If ##0<a<1##, then ##\lim_{x\rightarrow -\infty}{a^x=\infty}## and ##\lim_{x\rightarrow \infty}{a^x=0}##
The graph of ##y=a^x## has the x-axis as an horizontal asymptote if ##a\neq 1##. It is asymptotic on the left (as ##x\rightarrow{-\infty}##) if ##a>1## and on the right (as ##x\rightarrow{\infty}##) if ##0<a<1##
In my opinion, it is asymptotic on the left (as ##x\rightarrow{-\infty}##) if ##a>0## and on the right (as ##x\rightarrow{\infty}##) if ##a>0##. This remark doesn't contradict the texbook, but I think it is rather acccurate.
Greetings!
The logarithm is the inverse function to exponentiation. But, focusing on exponentiation, here comes the graph:

And, next, the quote
An exponential function is a function of the form ##f(x)=a^x##, where the base ##a## is a positive constant and the exponent ##x## is the variable.
Observe that ##a^x>0## for all ##a>0## and all real ##x## and that
If ##a>1##, then ##\lim_{x\rightarrow -\infty}{a^x=0}## and ##\lim_{x\rightarrow \infty}{a^x=\infty}##
If ##0<a<1##, then ##\lim_{x\rightarrow -\infty}{a^x=\infty}## and ##\lim_{x\rightarrow \infty}{a^x=0}##
The graph of ##y=a^x## has the x-axis as an horizontal asymptote if ##a\neq 1##. It is asymptotic on the left (as ##x\rightarrow{-\infty}##) if ##a>1## and on the right (as ##x\rightarrow{\infty}##) if ##0<a<1##
In my opinion, it is asymptotic on the left (as ##x\rightarrow{-\infty}##) if ##a>0## and on the right (as ##x\rightarrow{\infty}##) if ##a>0##. This remark doesn't contradict the texbook, but I think it is rather acccurate.
Greetings!