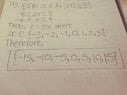Please check/confirm if the set is correct
- Thread starter Math100
- Start date
-
- Tags
- Set
Click For Summary
SUMMARY
The discussion focuses on confirming the correctness of a mathematical set defined by the expression {5x | x ∈ ℤ ∧ |2x| ≤ 8}. The correct interpretation includes the closed interval where both -4 and 4 are included, leading to the final set of {-20, -15, -10, -5, 0, 5, 10, 15, 20}. Participants emphasized the importance of presenting conclusions as statements rather than mere expressions, ensuring clarity in mathematical communication.
PREREQUISITES- Understanding of set notation and elements
- Familiarity with mathematical expressions involving integers (ℤ)
- Knowledge of absolute value concepts
- Ability to interpret and manipulate inequalities
- Study the properties of closed intervals in set theory
- Learn about set-builder notation and its applications
- Explore the implications of absolute values in mathematical expressions
- Practice writing and interpreting mathematical statements and conclusions
Students, educators, and anyone involved in mathematics who seeks to improve their understanding of set notation and precise mathematical communication.
Similar threads
- · Replies 11 ·
- · Replies 10 ·
- · Replies 6 ·
- · Replies 1 ·
- · Replies 2 ·
- · Replies 31 ·
- · Replies 9 ·