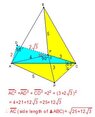
The problem involves finding the side length of an equilateral triangle ABC, given an inner point P with distances PA=4, PB=5, and PC=3. By rotating triangle ABC by 60 degrees around point C, the angle P'PA is established as 90 degrees, leading to the formation of triangle CPA with angle CPA measuring 150 degrees. This geometric configuration allows for the application of the Law of Cosines to derive the side length of triangle ABC.
PREREQUISITESMathematics students, geometry enthusiasts, and educators looking to deepen their understanding of triangle properties and problem-solving techniques.
Rotate the trianlge by 60 degrees about the point C. Let $P'$ be the new position of $P$. Then $\angle P'PA=90$. Thus we get a triangle $CPA$ with $\angle CPA=150$ and $PC=3, PA=4$. To find $AC$.Albert said:
Brilliant solution!Albert said:
