Pleeeease Help Why a dielectric absorbs only a certain amt of field

[jtbell]

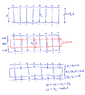
First consider a parallel-plate capacitor without a dielectric. The potential difference \Delta V = Ed where d is the distance between the plates.

Now put a dielectric inside the capacitor. The electric field inside the dielectric is weaker, call it E_2. Nevertheless, at the plates, which are still outside the dielectric, the electric field is still E. (Imagine that the dielectric is very slightly narrower than the capacitor, so there is still a very small gap between the dielectric and the plates.)

The potential difference is now \Delta V_2 = E_2 d, which is less than the original \Delta V.

 

[LHarriger]

Why do you think that there is no electric field on the other side of an insulator from the field's source?

I think I might know the source of the misunderstanding here. The electric field due to charged parallel plates is confined to only the region between the plates (excluding any discussion about fringing fields, which must exist for the curl of E to be zero). This field confinement is true regardless of whether there is a dielectric between the plates and is due to the special geometry of the situation. It does not apply to other charge configurations. When thinking in terms of capacitors I could see how someone could wrongly imagine dielectrics as "draining away" all of the electric field so that nothing reaches the other side. In reality the field drop for a dielectic of any geometry is confined to only the region inside the dielectric. The situation is actually the opposite on the outside! The polarization of the dielectric produces an electric field in the same direction as the applied field that produced it, thus increasing the overall field.

 

[Mr Virtual]

The polarization of the dielectric produces an electric field in the same direction as the applied field that produced it, thus increasing the overall field.

I don't think I agree with you on this point. A dielectric does "consume" (or oppose) the applied field, reducing its value. The cell has to do some work to return the value of V to its original value.
Suppose we have fully charged a capacitor (having air as dielectric) to potential V, and disconnected it from battery. If we now insert a dielectric in between the plates, there will be a drop in potential V, because there is a drop in field E. If we introduce a conductor instead (not touching any of the two plates), then there will be no drop in potential. If we introduce an insulator instead, V will drop but negligibly.
Perhaps you were saying that if we connect the battery, then reduced electric field again regains its original value. But this value does not go beyond the value of the original field of the capacitor when it was charged initially.

Mr V

 

[LHarriger]

Suppose we have fully charged a capacitor (having air as dielectric) to potential V, and disconnected it from battery. If we now insert a dielectric in between the plates, there will be a drop in potential V, because there is a drop in field E.

Agree

If we introduce a conductor instead (not touching any of the two plates), then there will be no drop in potential.

Agree

If we introduce an insulator instead, V will drop but negligibly.

Agree

Perhaps you were saying that if we connect the battery, then reduced electric field again regains its original value. But this value does not go beyond the value of the original field of the capacitor when it was charged initially.

Mr V

No, that's not what I am saying.
But I will admit to some sloppiness in my previous post:
First, when a dielectric feels an applied electric field, then this causes a polarization of its molecules or atoms. It is these dipole moments that point in the same direction as the applied field (not neccesarily the external induced field as I stated in my previous post.) For most atoms, the dipole moment is approximately proportional to E which allows us to relate the dipole moment to the field as:

\vec{E} = \alpha \vec{p}

where \alpha is called the atomic polarizability of the atom.
However, these induced dipole moments have their own electric field. This induced field is what I was referring to earlier. The potential for this field is given by

V(\vec{r}) = \frac{1}{4\pi\eplison_{0}}\frac{\hat{R} \cdot \vec{p}}{R^{2}}

However, this is only for a single dipole. When you integrate over all of the dipoles, you find that they result in a bound surface charge and a bound volume charge for the entire dielectric. The field induced by this entire bound charge is different depending on where you look.
Inside the dielectric the induced field is in the opposite direction of the applied field. This results in the reduction of the overall field.
Outside of the dielectric the induced field is (more or less) in the same direction as the applied field in many regions. Which results in a total electric field which is greater than the original applied field.
At some point in an undergraduate E&M course you should work a problem where you first calculate the polarization of the dielectic due to only the applied field, then adjust this result to include a futher polarization of the dielectric due to the first polarization, this in turn causes yet a further polarization...ad infinitum. The final solution is the sum of an infinite geometric series. I think if you come to understand the structure and origin of this induced field then it will clear up a lot of confusion.

 

[Mr Virtual]

I still don't understand what you're trying to explain to me (forgive me for being so dumb). But this was not what I intended to ask. All I want to know is: if the internal field of the insulator is negligible, then applied field should not reduce dramatically, and almost all of it should reach the other plate of the capacitor. Which means potential V of the capacitor also does not drop drastically, which means an insulator is not a good choice for a capacitor, because it stores extremely small amount of energy (if any at all). Whereas a dielectric strongly opposes the applied field, leading to drop in field and in V, and thus, it stores considerable energy (due to stretching). Am I right?

Mr V

 

[jtbell]

Perhaps the attached diagram will help. It shows the electric field before and after inserting a dielectric into a capacitor, and how the potential difference across the capacitor is calculated in both cases.

The arrows are electric field lines, not vectors. The strength of the electric field is proportional to the number of field lines, not to their length. The original electric field is E_0. When the dielectric is inserted, the polarization induces an effective electric charge on the surfaces of the dielectric, which produces an additional induced electric field E_i inside the dielectric. For this example I assume that E_i = E_0 / 2. The net electric field inside the dielectric is E_0 - E_i.

The + and - represent the charge on the capacitor and the induced charge on the surfaces of the dielectric.

The final result is that the potential difference \Delta V across the capacitor is reduced (in this example) from E_0 d to E_0 d - 0.6 E_i d. The 0.6 is a purely geometrical factor. It appears because I chose the dielectric to fill 0.6 of the space between the capacitor plates. If you expand the dielectric to fill more and more of the space, this factor increases accordingly, until it reaches 1.0 when the dielectric fills the space completely.

 

[Mr Virtual]

I really appreciate and thank you that you took out time to draw the diagram.
But my question is still unanswered. A field Eo is applied across the two plates of a capacitor. When we introduce a dielectric, an induced field Ei builds up which opposes Eo, thus reducing it to E. Here, E<Eo. Now suppose that we introduce an insulator inside the capacitor. The molecules of the insulator barely stretch, so Ei is negligible. Thus, when we do E=Eo-Ei, then E~Eo (i.e. E should approx equal Eo). Is this right or wrong?

Mr V

 

[jtbell]

A dielectric is an insulator! If it were not an insulator, that is, a conductor, there would be an electric current through the capacitor and it wouldn't be a capacitor any more!

What you're describing is a dielectric with a vanishing dielectric constant. Such a material indeed would not be very useful as a dielectric. But good dielectrics with high dielectric constants are nevertheless still insulators.

The fact that a dielectric gets an induced polarization when immersed in an electric field does not make it a conductor. What makes a material a conductor is that some of its electrons are not bound to any particular atom but instead can roam throughout the material. In an insulator, all the electrons are bound to particular atoms, but in general they can still shift their average position very slightly with respect to their nucleus, so the atoms are polarizable. Some kinds of atoms or molecules are more polarizable than others, so they make better dielectrics.

 

[Mr Virtual]

I am very much clear about what you have told me. I am stating the words 'dielectric' and 'insulator' just to indicate (yes! you guessed it right) the diminishing dielectric constant. Perhaps I was using wrong words which was giving you such an impression.
But thanks a LOT! I have finally got the answer I have been trying to get for the last one month ( I started this thread on 6 June)!

Such a material indeed would not be very useful as a dielectric.

This was what I needed. So an insulator (please forgive me for my choice of words) stops flow of electrons through it, but does a bad job in blocking the field. Most of the applied field just passes through it at the other end. On the other hand, a dielectric (or an insulator with a high dielectric constant) both stops flow of electrons and blocks a considerable amount of field (due to polarization).

Thanks, thanks, thanks, once again!

 

[jtbell]

OK, I see where our confusion lies now. We're using the word "insulator" to mean different things. To me, "insulator" simply means something that blocks the flow of electric current, without regard for its properties as a dielectric. You were apparently using "insulator" to mean something that also has a high dielectric constant.

 

[Mr Virtual]

You were apparently using "insulator" to mean something that also has a high dielectric constant.

A low dielectric constant (not high) is what you mean, isn't it?

Mr V