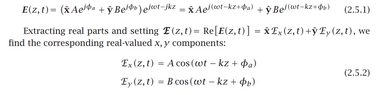yefj
- 58
- 2
- Homework Statement
- plotting EM polarized wave in matlab
- Relevant Equations
- polarization ellipse
Hello , there is a polarization matix I want to implement in matlab.
I have build a basic matlab plot which could visualize EM waves in 3D.
The basic equations described in equation 2.5.1 from the attached link.
given the simple case of linear polarization, What is the strategy of plotting 2.5.1 EM representation like in the photo below?
Thanks.
https://eceweb1.rutgers.edu/~orfanidi/ewa/ch02.pdf


[CODE lang="matlab" title="matlab 3D wave plot"]clc
clear
x = linspace(0,4*pi,100);
figure;
plot3(x,zeros(1,100),zeros(1,100),'k','LineWidth',2);
hold on
plot3(x,-sin(x),zeros(1,100),'k');
plot3(x,zeros(1,100),sin(x),'k');
x_quiver = 0:pi/4:4*pi;
q1 = quiver3(x_quiver,zeros(1,17),zeros(1,17),zeros(1,17),-sin(x_quiver),zeros(1,17),0);
q2 = quiver3(x_quiver,zeros(1,17),zeros(1,17),zeros(1,17),zeros(1,17),sin(x_quiver),0);
hold off;
[/CODE]
I have build a basic matlab plot which could visualize EM waves in 3D.
The basic equations described in equation 2.5.1 from the attached link.
given the simple case of linear polarization, What is the strategy of plotting 2.5.1 EM representation like in the photo below?
Thanks.
https://eceweb1.rutgers.edu/~orfanidi/ewa/ch02.pdf
[CODE lang="matlab" title="matlab 3D wave plot"]clc
clear
x = linspace(0,4*pi,100);
figure;
plot3(x,zeros(1,100),zeros(1,100),'k','LineWidth',2);
hold on
plot3(x,-sin(x),zeros(1,100),'k');
plot3(x,zeros(1,100),sin(x),'k');
x_quiver = 0:pi/4:4*pi;
q1 = quiver3(x_quiver,zeros(1,17),zeros(1,17),zeros(1,17),-sin(x_quiver),zeros(1,17),0);
q2 = quiver3(x_quiver,zeros(1,17),zeros(1,17),zeros(1,17),zeros(1,17),sin(x_quiver),0);
hold off;
[/CODE]