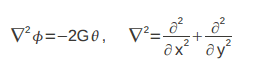SUMMARY
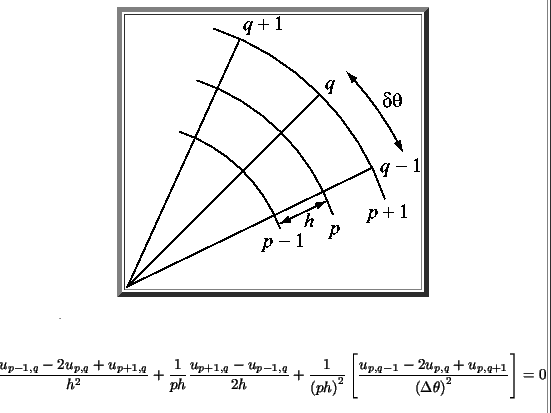
This discussion focuses on solving a Laplace Partial Differential Equation (PDE) in polar coordinates using the Finite Difference Method (FDM). The user seeks clarification on the implementation of boundary conditions and examples of practical applications. The Laplacian in polar coordinates is essential for this process, and the discussion references a Wikipedia article for foundational knowledge. A clear example of the solution process is requested to enhance understanding.
PREREQUISITES
- Understanding of Laplace Partial Differential Equations
- Familiarity with Finite Difference Method (FDM)
- Knowledge of polar coordinate systems
- Basic grasp of boundary conditions in PDEs
NEXT STEPS
- Study the derivation of the Laplacian in polar coordinates
- Explore detailed examples of Finite Difference Method applications
- Research boundary condition techniques for PDEs
- Examine numerical stability and convergence in FDM
USEFUL FOR
Mathematicians, physicists, and engineers interested in numerical methods for solving PDEs, particularly those working with polar coordinate systems and the Finite Difference Method.