Polar Definition and 1000 Threads

The American Anthropological Association (AAA) is an organization of scholars and practitioners in the field of anthropology. With 10,000 members, the association, based in Arlington, Virginia, includes archaeologists, cultural anthropologists, biological (or physical) anthropologists, linguistic anthropologists, linguists, medical anthropologists and applied anthropologists in universities and colleges, research institutions, government agencies, museums, corporations and non-profits throughout the world. The AAA publishes more than 20 peer-reviewed scholarly journals, available in print and online through AnthroSource. The AAA was founded in 1902.

View More On Wikipedia.org
Recent contents Top users
  1. brotherbobby

    B To calculate the polar unit vectors using rotated coordinates

    We know that if cartesian coordinates ##(x,y)## (see figure alongside) are rotated to ##(x',y')## about the origin by an angle ##\theta## counter-clockwise as shown, the rotated coordinates are given by $$\begin{align*}x'&=\cos\theta \;x+\sin\theta \;y\\ y'&=-\sin\theta \; x+\cos\theta \; y...
  2. J

    I Units of a vector in a velocity vs time graph?

    This post parallels a post I made in electrical engineering regarding the S plane. I thought I would post an equivalent in basic physics. So, given a graph of velocity vs time we have on the vertical axis meters/sec and the hormonal axis just meters. Given a plot of V vs t we know the area...
  3. chwala

    Show proof of point C in the given problem that involves Polar equation

    c Parts (a) and (b) are okay ... though the challenge was on part (a) My graph had a plot of r on the y-axis vs θ on the x-axis). The sketch of my graph looks like is shown below; I suspect the ms had θ on the x-axis vs r on the y-axis. I used the equation ##r=\sqrt{\dfrac {1}{θ^2+1}}##...
  4. E

    Help please with De Moivre's Theorem (raising a complex number to a power)

    Hi all any help on this would be great I cant seem to progress with the theorem, z= -2 + j > R sqrt (-2)'2 + (-1)'2 r = 2.24 0= Arctan(-1) = 26.57 Polar form = 2.24(cos(26.58)+jsin(26.58) -2 Demoivre - (cos0+jsin0)'n = cosn0 +jsinno Could some one...
  5. DaraRychenkova

    Optimizing Polar Axis for Dipole in Polar Coordinates

    I don't know how to get the result referring to the previous task. Is my decision correct?
  6. R

    A Converting this vector into polar form

    In the following%3A%20https://pubs.rsc.org/en/content/articlehtml/2013/sm/c3sm00140g?casa_token=3O_jwMdswQQAAAAA%3AaSRtvg3XUHSnUwFKEDo01etmudxmMm8lcU4dIUSkJ52Hzitv2c_RSQJYsoHE1Bm2ubZ3sdt6mq5S-w'] paper, the surface velocity for a moving, spherical particle is given as (eq 1)...
  7. mncyapntsi

    Confused about polar integrals and setting up bounds

    So I want to subtract the two surfaces, right? I really don't know where to start... I am guessing this would be some sort of triple integral, however I am very confused with the bounds. Any help would be greatly appreciated! Thanks!!
  8. neilparker62

    Non polar molecule with polar bonds?

    Consider for example Carbon Dioxide. Oxygen is more electronegative than carbon so should obtain the "lion's share" of the paired electrons in the double bonds. But (as I see it anyway) the oxygen atoms on either side of the central carbon "assist" the carbon atom to maintain an even share of...
  9. H

    A Polar Fourier transform of derivatives

    The 2D Fourier transform is given by: \hat{f}(k,l)=\int_{\mathbb{R}^{2}}f(x,y)e^{-ikx-ily}dxdy In terms of polar co-ordinates: \hat{f}(\rho,\phi)=\int_{0}^{\infty}\int_{-\pi}^{\pi}rf(r,\theta)e^{-ir\rho\cos(\theta-\phi)}drd\theta For Fourier transforms in cartesian co-ordinates, relating the...
  10. T

    Integration of acceleration in polar coordinates

    I made this exercise up to acquire more skill with polar coordinates. The idea is you're given the acceleration vector and have to find the position vector corresponding to it, working in reverse of the image. My attempts are the following, I proceed using 3 "independent" methods just as you...
  11. R

    Polar and non-polar compounds and their solubility

    Hi Please can anyone explain why Naphthalene is soluble in liquid Ammonia when Naphthalene is Non-polar and Ammonia is Polar?
  12. J

    Calculating the partial derivative in polar coordinates

    Hello, I am trying to solve the following problem: If ##z=f(x,y)##, where ##x=rcos\theta## and ##y=rsin\theta##, find ##\frac {\partial z} {\partial r}## and ##\frac {\partial z} {\partial \theta}## and show that ##\left( \frac {\partial z} {\partial x}\right){^2}+\left( \frac {\partial z}...
  13. K

    I Wavefunction in polar coordinates and its bra ket notation

    The wavefunction of ##|\psi\rangle## is given by the bra ket ##\psi (x,y,z)= \langle r| \psi\rangle## I can convert the wavefunction from Cartesian to polar and have the wavefunction as ## \psi (r,\theta,\phi)## What bra should act on the ket ##|\psi\rangle## to give me the wavefunction as ##...
  14. Father_Ing

    Cartesian and polar coordinate in Simple pendulum, Euler-Lagrange

    $$L = \frac {mv^2}{2} - mgy$$ It is clear that ##\dot{x}=\dot{\theta}L## and ##y=-Lcos \theta##. After substituting these two equations to Lagrange equation, we will get the answer by simply using this equation: $$\frac {d} {dt} \frac {∂L}{∂\dot{\theta}} - \frac {∂L}{∂\theta }= 0$$ But, What if...
  15. D

    How Is Polar to Rectangular Conversion Used in Complex Number Calculations?

    I'm having trouble trying to calculate how the answer below was achieved from an example i have seen, see below: 208L0 - 2.5L90 x 27.42L36.9 which is then calculated to 255.12L-12.4. I have tried converting everything to rectangular form, subtract where required and the convert back to polar...
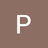
  16. Stefan H

    A Solving Laplace's equation in polar coordinates for specific boundary conditions

    Hello everybody, Currently I am doing my master's thesis and I've encountered a physics problem which is very difficult for me to solve. The problem I have is finding equations for the magnetic scalar potential inside and outside a ferromagnetic wire for specific boundary conditions...
  17. uzi kiko

    Python Numerical integration over a disk with polar coordinates

    In my job, I was given the task of calculating a force that operates an ultrasound transmitter on a receiver. The calculation is made by assuming that each point on the transmitter is a small transmitter and integration should be made on the surface of the transmitter. Since the transmitter is...
  18. ektov_konstantin

    I Moving center of coordinates in the polar graph

    I have a function in polar coordinates: t (rho, phi) = H^2 / (H^2 + rho^2) (1) I have moved the center to the right and want to get the new formulae. I use cartesian coordinates to simplify the transformation (L =...
  19. derya

    A Analytical solution for an integral in polar coordinates?

    Hi, I am trying to find open-form solutions to the integrals attached below. Lambda and Eta are positive, known constants, smaller than 10 (if it helps). I would appreciate any help! Thank you!
  20. M

    I Transform from polar to cartesian

    Probability distribution - uniform on unit circle. In polar coordinates ##dg(r,a)=\frac{1}{2\pi}\delta(r-1)rdrda##. This transforms in ##df(x,y)=\frac{1}{2\pi}\delta(\sqrt{x^2+y^2}-1)dxdy##. The problem I ran into was the second integral was 1/2 instead of 1.
  21. A

    Double integral with polar coordinates

    Greetings! I have the following integral and here is the solution of the book (which I understand perfectly) I have an altenative method I want to apply that does not seems to gives me the final resultMy method which doesn't give me the final results! where is my mistake? thank you!
  22. George Keeling

    LaTeX Plane polar noncoordinate basis (Latex fixed)

    I am trying to do exercise 8.5 from Misner Thorne and Wheeler and am a bit stuck on part (d). There seem to be some typos and I would rewrite the first part of question (d) as follows Verify that the noncoordinate basis ##{e}_{\hat{r}}\equiv{e}_r=\frac{\partial\mathcal{P}}{\partial r},\...
  23. P

    Polar Covalent Bond in HCl question

    If my understanding is correct, the polar covalent bond in HCl creates a polar molecule because the molecule is unsymmetrical. 1. Does this mean that the partially positive H of one HCl molecule will be attracted to the partially negative Cl of another HCl molecule and vice versa, to create a...
  24. J

    Electronics Will this electronic circuit work? (back-to-back polar capacitors)

    All I need is for someone to look at my schematic and tell me if this circuit will work. Thanks.
  25. I

    Polar Ice Caps and the Earth's Speed of Rotation

    Is it correct to say that the melting of the polar caps due to climate change may increase Earth's speed of rotation?
  26. CPW

    Acceleration in Polar Coords, Intuitive Definition video

    Summary:: I wish this video (and YouTube in general) was around when I took intermediate level mechanics as an undergraduate physics student: I wish this video (and YouTube in general) was around when I took intermediate level mechanics as an undergraduate physics student:
  27. D

    I Vector squared in polar coordinates

    Hi I was always under the impression that i could write a2 = a.a = a2 Equation 1 where a⋅ is a vector and a is its modulus but when it comes to the kinetic energy term for a particle in plane polar coordinates I'm confused ( i apologise here as i don't know how to write time derivative with...
  28. Leo Liu

    Computing the polar moment of inertia (calculus)

    Question: Diagram: So the common approach to this problem is using polar coordinates. The definition of infinitesimal rotational inertia at O is ##dI_O=r^2\sigma\, dA##. Therefore the r. inertia of the triangle is $$I_O=\int_{0}^{\pi/3}\int_{0}^{\sec\theta}r^2r\,drd\theta$$ whose value is...
  29. warhammer

    Basic question pertaining to Polar Coordinates & how to employ them

    I have a question that might be considered vague or even downright idiotic but just wanted to know that once we find out the velocity & acceleration of a body in angular motion in plane polar coordinates, and are asked to integrate the expressions in order to find position at some specified time...
  30. yucheng

    Incorrect derivation of tangential acceleration in polar coordinates

    I am trying to derive the tangential acceleration of a particle. We have tangential velocity, radius and angular velocity. $$v_{tangential}= \omega r$$ then by multiplication rule, $$\dot v_{tangential} = a_{tangential} = \dot \omega r + \omega \dot r$$ and $$a_{tangential} = \ddot \theta r +...
  31. I

    How can the vertices of an ellipse be found using polar equations?

    The text says that the following conic, r = 15/[3-2cos(theta)], can be rearranged to 5/[1-(2/3)cos(theta)]. The graph of the conic is an ellipse with e=2/3. Then it says that the vertices lie at (15,0) and (3,pi). How did they find the vertices? Thanks.
  32. R

    MHB How Do You Solve Problems in Polar Coordinates?

    I need a little help with this problem please
  33. P

    Help graphing Vectors in polar form

    The equation I'm trying to graph on desmos is this with A & B as numbers, but I'm unsure how as it is a vector. r = (A cosθ sinθ cscθ - B sinθ cscθ) i + (A cosθ sinθ cscθ + B sinθ cscθ) j
  34. srfriggen

    I Cartesian to Polar form.... Is it just a transformation of the plane?

    Hello, Today I started to think about why graphs, of the same equation, look different on the Cartesian plane vs. the polar grid. I have this visualization where every point on the cartesian plane gets mapped to a point on the polar grid through a transformation of the grids themselves...
  35. F

    I Plotting polar equations and scale invariance

    Hello, In the plane, using Cartesian coordinates ##x## and ##y##, an equation (or a function) is a relationship between the ##x## and ##y## variables expressed as ##y=f(x)##. The variable ##y## is usually the dependent variable while ##x## is the independent variable. The polar coordinates...
  36. randomphysicsguy123

    Vector Problem -- Addition of two vectors given in polar coordinates

    Doing a review for my SAT Physics test and I'm practicing vectors. However, I am lost on this problem I know I need to use trigonometry to get the lengths then use c^2=a^2+b^2. But I need help going about this.
  37. JorgeM

    A How do I express an equation in Polar coordinates as a Cartesian one.

    I got a polar function. $$ \psi = P(\theta )R(r) $$ When I calculate the Laplacian: $$ \ \vec \nabla^2 \psi = P(\theta)R^{\prime\prime}(r) + \frac{P(\theta)R^{\prime}(r)}{r} + \frac{R(r)P^{\prime\prime}(\theta)}{r^{2}} $$ Now I need to convert this one into cartesian coordinates and then...
  38. patric44

    Orthogonal trajectories in polar coordinates

    there is a problem in a book that asks to find the orthogonal trajectories to the curves described by the equation : $$r^{2} = a^{2}\cos(\theta)$$ the attempt of a solution is as following : 1- i defferntiate with respect to ##\theta## : $$2r \frac{dr}{d\theta} = -a^{2}\;\sin(\theta)$$ 2- i...
  39. A

    Complex numbers: convert the exponential to polar form

    Summary:: Hello, my question asks if the complex exponential equation 4e^(-j) is equal to 4 ∠-180°. I tried to use polar/rectangular conversions: a+bj=c∠θ with c=(√a^2 +b^2) and θ=tan^(-1)[b/a] 4e^(-j)=4 ∠-180° c=4, 4=(√a^2 +b^2) solving for a : a=(√16-b^2) θ=tan^(-1)[b/a]= -1 b/(√16-b^2)=...
  40. M

    Stokes' Theorem 'corollary' integral in cylindrical polar coordinates

    Hi, I was just working on a homework problem where the first part is about proving some formula related to Stokes' Theorem. If we have a vector \vec a = U \vec b , where \vec b is a constant vector, then we can get from Stokes' theorem to the following: \iint_S U \vec{dS} = \iiint_V \nabla...
  41. A

    Where to use polar (cylindrical coor.) in double and triple integrals

    where the region of integration is the cube [0,1]x[0,1]x[0,1] my question is where can we use the polar coordinate? is it only usable if the region of integration looks like a circle regardless of the function inside the integral? (if yes it means that using this kind of transformation is wrong...
  42. W

    I Using polar coordinates to describe rose petals

    I encountered a question which asked me to describe the rose petal sketched below in polar coordinates. The complete answer is R = {(r, θ): 0 ≤ r ≤ 6 cos(3θ), 0 ≤ θ ≤ π}. That makes sense to me for the right petal. What about the other two on the left?
  43. T

    Orbital equations in polar coordinates

    The equations of motion are: \ddot{r}-r{\dot{\theta}} ^{2} = -\frac{1}{r^{2}} for the radial acceleration and r\ddot{\theta} + 2\dot{r}\dot{\theta}= 0 for the transverse acceleration When I integrate these equations I get only circles. The energy of the system is constant and the angular...
  44. J

    MHB Finding the Unique Solution of a Polar System with Variable Radius?

    Hello! Brand new to the forums, hopefully someone here can help me out. Paths start out at the edge of a circle and "flow" along a polar equation that determines phi based off the initial phi (phi0) and a variable radius (ie. as your radius grows, your phi is changing). Hopefully this image...
  45. P

    Polar coordinates of the centroid of a uniform sector

    If I use cartesian co-ordinates, I get: ##\bar{x}=\frac{1}{A}\iint x\, dA=\frac{1}{A} \iint r^2\cos\theta\, dr\, d\theta= \frac{2a\sin\theta}{3\theta}## ##\bar{y}=\frac{1}{A}\iint y\, dA=\frac{1}{A}\iint r^2\sin\theta\, dr\, d\theta= \frac{2a(1-\cos\theta)}{3\theta}## But if I use polar...
  46. Leo Liu

    A particle moving with zero radial acceleration in polar coordinates

    In the example above, the authors claim that when ##r=r_0e^{\beta t}##, the radial acceleration of the particle is 0. I don't quite understand it because they did not assume ##\beta=\pm \omega##. Can anyone please explain it to me? Many thanks.
  47. Leo Liu

    Insight into polar coordinates (Newtonian mechanics)?

    I am learning to use polar coordinates to describe the motions of particles. Now I know how to use polar coordinates to solve problems and the derivations of many equations. However, the big picture of polar coordinates remains unclear to me. Would you mind sharing your insight with me so that I...
  48. Kaguro

    What is the issue with the polar acceleration problem?

    ##\vec r=r \hat r## ##\vec v=\dot r \hat r + r \dot \theta \hat \theta## ##\vec a = (\ddot r - r \dot \theta^2)\hat r + (2 \dot r \dot \theta + r \ddot \theta)\hat \theta## Given that, ##2 \dot r \dot \theta + r \ddot \theta =0## Also, ##r \theta=constant## ##\Rightarrow \dot r \theta + r \dot...
  49. Leo Liu

    Is the length of the arm r in a polar coordinate a function of the angle?

    My textbook says ##\vec r (\theta) = r \hat r (\theta)##, where ##\hat r (\theta)## is the terminal arm (a position vector in some sense). It can be seen that both ##\vec r (\theta)## and ##\hat r (\theta) ## are function of ##\theta##; whereas, the length of the vector ##r## is not. I...
  50. Astrowolf_13

    Find the area delimited by two polar curves

    I attempted to solve this problem by finding the angles of an intersection point by equalling both ##r=sin(\theta)## and ##r=\sqrt 3*cos(\theta)##. The angle of the first intersection point is pi/3. The second intersection point is, obviously, at the pole point (if theta=0 for the sine curve and...
Back
Top