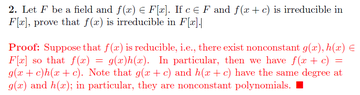Polynomial Proof: Verification & Correction

  • Context: MHB 
  • Thread starter Thread starter Joe20
  • Start date Start date
  • Tags Tags
    Polynomial Proof
Click For Summary
SUMMARY

The forum discussion centers on the verification of a polynomial proof presented by a user named Alexis87. A participant confirms the correctness of the proof but suggests adding a concluding statement to clarify that f(x+c) is reducible, which leads to a contradiction. This addition enhances the proof's clarity and strengthens its argument. Overall, the discussion emphasizes the importance of clear conclusions in mathematical proofs.

PREREQUISITES
  • Understanding of polynomial functions and their properties
  • Familiarity with mathematical proof techniques
  • Knowledge of reducibility in algebraic expressions
  • Basic experience with logical reasoning in mathematics
NEXT STEPS
  • Research the concept of polynomial reducibility in algebra
  • Study techniques for writing clear mathematical proofs
  • Explore common pitfalls in polynomial proof verification
  • Learn about the implications of contradictions in mathematical arguments
USEFUL FOR

Mathematicians, students studying algebra, educators teaching proof techniques, and anyone interested in enhancing their understanding of polynomial functions and proof verification.

Joe20
Messages
53
Reaction score
1
I would like to have verification if the following attached proof is correct. If it is not correct, what can be done to make it correct? Thanks.
 

Attachments

  • pp.png
    pp.png
    15.4 KB · Views: 97
Physics news on Phys.org
Alexis87 said:
I would like to have verification if the following attached proof is correct. If it is not correct, what can be done to make it correct? Thanks.

Hi Alexis87,

It looks all correct to me.
For clarity I would just add a final sentence saying that therefore f(x+c) is reducible, which is a contradiction.
 

Similar threads

Undergrad Analogy question for algebraists
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Solve the problem involving Rings
  • · Replies 5 ·
Replies
5
Views
2K
MHB Solve Part (b) of Nonzero Polynomials | Help Needed
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad Quintic Polynomial Tschirnhaus Transform: Possible complex Bring Radicals
  • · Replies 0 ·
Replies
0
Views
2K
Undergrad What Conditions Ensure the Minimal Polynomial of α Divides P in Galois Theory?
  • · Replies 12 ·
Replies
12
Views
3K
Undergrad Uniqueness of reduced row echelon form (proof verification)
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Use of induction in the proof of the Chinese Remainder Theorem
  • · Replies 7 ·
Replies
7
Views
3K
Undergrad Separable Polynomials - Remarks by Dummit and Foote .... ....
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Localizing single variable quotient polynomial ring at a prime ideal
  • · Replies 6 ·
Replies
6
Views
1K
MHB Ideals and Ker(f) Solution for (a), (b), and (c)
  • · Replies 12 ·
Replies
12
Views
2K